
����Ŀ����P����dֵ���������£�����QΪԲ������һ�㣬�߶�PQ���ȵ����ֵ����Сֵ֮�Ϊ��P����dֵ������ΪdP���ر�ģ�����P��Q�غ�ʱ���߶�PQ�ij���Ϊ0������O�İ뾶Ϊ2ʱ��
��1������C����![]() ��0����D��3��4������dc=�� ����dp=�� ����
��0����D��3��4������dc=�� ����dp=�� ����
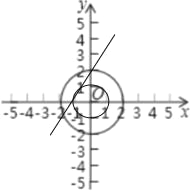
��2������ֱ��y=2x+2�ϴ��ڵ�P��ʹ��dP=2�������P�ĺ����ꣻ
��3��ֱ��y=��![]() x+b��b��0����x�ᣬy��ֱ��ڵ�A��B�����߶�AB�ϴ��ڵ�P��ʹ��2��dP��3������ֱ��д��b��ȡֵ��Χ��
x+b��b��0����x�ᣬy��ֱ��ڵ�A��B�����߶�AB�ϴ��ڵ�P��ʹ��2��dP��3������ֱ��д��b��ȡֵ��Χ��
���𰸡���1��1��4����2��P�ĺ�����Ϊ��1��![]() ����3��
����3��![]() ��b��
��b��![]() ��
��
��������
��1��Բ�ڵĵ��dֵ=����㵽Բ�ľ����2����Բ�ϻ�Բ��ĵ��dֵ=Բ��ֱ�����ɴ˼��ɽ�����⣻
��2���������⣬����dp=2�ĵ�λ�ڡ�O�ڲ���������OΪԲ�İ뾶Ϊ1��Բ�ϣ����Լ���P��a��2a+2��������PO=1���������̼��ɽ�����⣻
��3���������⣬����2��dP��3�ĵ�λ�ڵ�OΪԲ���⾶Ϊ![]() ���ھ�Ϊ1��Բ���ڣ��ֲ������Բ���߶�AB����ʱb��ֵ���ɽ�����⣻
���ھ�Ϊ1��Բ���ڣ��ֲ������Բ���߶�AB����ʱb��ֵ���ɽ�����⣻
�⣺��1����������ɵ�Բ�ڵĵ��dֵ=����㵽Բ�ľ����2����Բ�ϻ�Բ��ĵ��dֵ=Բ��ֱ��������dc=1��dp=4��
�ʴ�Ϊ1��4��
��2���������⣬����dp=2�ĵ�λ����O�ڲ���������OΪԲ�İ뾶Ϊ1��Բ�ϣ�
����P��ֱ��y=2x+2�ϣ������Լ���P��a��2a+2����
��PO=1��
��a2+��2a+2��2=1��
���a=��1��![]() ��
��
�����������ĵ�P�ĺ�����Ϊ��1��![]() ��
��
��3���������⣬����2��dP��3�ĵ�λ�ڵ�OΪԲ���⾶Ϊ![]() ���ھ�Ϊ1��Բ���ڣ�
���ھ�Ϊ1��Բ���ڣ�
���߶��������ʱ���ɵ�b=![]() ��
��
���߶����ڻ�����ʱ���ɵ�b=![]() ��
��
��������������b��ֵ��![]() ��b��
��b��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ�˹��������Լ��ˮ������ʵ�������շ��ƶȣ���ÿ����ˮ��������14�֣���14�֣�����ÿ�ְ����������Żݼ�mԪ�շѣ���ÿ����ˮ������14�֣�������ÿ�ְ��г���nԪ�շѣ�С����3�·���ˮ20�֣���ˮ��49Ԫ��4�·���ˮ18�֣���ˮ��42Ԫ��
��1����ÿ��ˮ�����������Żݼۺ��г��۷ֱ��Ƕ��٣�
��2����ÿ����ˮ��Ϊx�֣�x>14����Ӧ��ˮ��ΪyԪ����д��y��x֮��ĺ�����ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
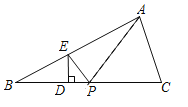
����Ŀ����ͼ����ABC���ܳ�Ϊ28����D��E���ڱ�BC�ϣ���ABC��ƽ���ߴ�ֱ��AE������ΪQ����ACB��ƽ���ߴ�ֱ��AD������ΪP����BC��12����PQ�ij�Ϊ��������
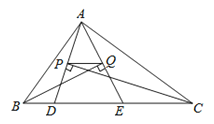
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�����⣺
�����θ��ͣ�
��������ͼ1��![]() ��ֱ��
��ֱ��![]() ͬ�Ե��������㣮
ͬ�Ե��������㣮
���⣺��ֱ��![]() ��ȷ��һ��
��ȷ��һ��![]() ��ʹ
��ʹ![]() ��ֵ��С��
��ֵ��С��
����������![]() ����ֱ��
����ֱ��![]() �ԳƵ�
�ԳƵ�![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ,
,
��������֮�䣬�߶��������֪����![]() ��Ϊ����ĵ㣮
��Ϊ����ĵ㣮
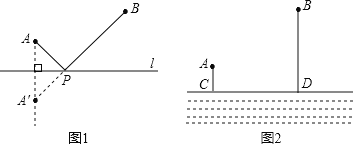
��ģ��Ӧ�ã�
��ͼ2��ʾ������![]() ��һ����
��һ����![]() ��ͬ�࣬
��ͬ�࣬![]() ���嵽�ӱ�
���嵽�ӱ�![]() �ľ���ֱ���
�ľ���ֱ���![]() ǧ��,
ǧ��,![]() ǧ��,
ǧ��, ![]() ǧ�ף���Ҫ�ںӱ�
ǧ�ף���Ҫ�ںӱ�![]() �Ͻ���һˮ������
�Ͻ���һˮ������![]() ������ˮ������ˮ�ܵĹ��̷���Ϊÿǧ��20000Ԫ��������
������ˮ������ˮ�ܵĹ��̷���Ϊÿǧ��20000Ԫ��������![]() ��ѡ��ˮ��λ�ã�ʹ����ˮ�ܵķ�����ʡ���������ʡ������ˮ�ܵķ���
��ѡ��ˮ��λ�ã�ʹ����ˮ�ܵķ�����ʡ���������ʡ������ˮ�ܵķ���![]() ��
��
����չ���죩
��ͼ��![]() �У���
�У���![]() �ڱ�
�ڱ�![]() �ϣ���
�ϣ���![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() Ϊ
Ϊ![]() ��һ�����㣬����
��һ�����㣬����![]() ����
����![]() �������
��С�����![]() Ӧ�����㣨 ����Ψһѡ����ȷ��
Ӧ�����㣨 ����Ψһѡ����ȷ��
A�� ![]() B��
B�� ![]()
C�� ![]() D��
D�� ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ʦ�����ó�Ϊ80��դ�����ٽ�����ѧ¥����ǽΧ��һ�����εĻ��![]() . ��֪��ѧ¥��ǽ��50�ף������
. ��֪��ѧ¥��ǽ��50�ף������![]() �ı�
�ı�![]() �ף����Ϊ
�ף����Ϊ![]() ƽ����.
ƽ����.
��1�����������![]() ��
��![]() ֮��Ĺ�ϵʽ����ָ��
֮��Ĺ�ϵʽ����ָ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����![]() Ϊ������ʱ��������������������Ƕ��٣�
Ϊ������ʱ��������������������Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڻ���ϣ�С����С�������һ�����ǰ�������ѧУ��˸߶ȣ���֪С�����۾������ľ��루AB����1.7m���������Լ���λ�ã��跨ʹ�����ǰ��һ��ֱ�DZ߱���ˮƽ����б������˶���M��ͬһ��ֱ���ϣ������˶���M����Ϊ45�㣻С����۾������ľ��루CD����1.5m����ͬ���ķ��������˶���M������Ϊ30�㣮�������28����λ��������ࣨ��B��N��D��ͬһ��ֱ���ϣ���������MN�ĸ߶ȣ����ο����ݣ� ![]() �����������������
�����������������
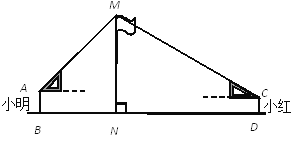
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A��B�������150ǧ�ף��ֱ��A��B����ù��Ҽ��羰������C���ķ�λ����ͼ��ʾ���羰����������CΪԲ�ģ�45ǧ��Ϊ�뾶��Բ��tan��=1.627��tan��=1.373��Ϊ�˿������Σ��йز������������AB���еĸ��ٹ�·��������AB���ٹ�·�Ƿ��羰������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijһ�죬С����С������һ�ӱߣ�����ƽ�澵��Ƥ�߲��������ӵĴ��¿��ȣ�������ȷ���ް�ȫ����������£����ںӰ���ѡ����һ��C����C��Ӷ������ϵ�һ�����ĵײ���B��ȷ����ֱ�ߴ�ֱ�ںӰ�����С����F��ʱ������ƽ�澵�п�������A��С���ڵ�D����ƽ�澵��С����H��ʱ������ƽ�澵�п�������A����F��D��H����BC���ӳ����ϣ�С�����۾������ĸ߶�EF=1.5m��С�����۾������ĸ߶�GH=1.6m�����CF=1m��DH=2m��CD=8.4m��AB��BH��EF��BH��GH��BH���������ϲ������̼��������ݣ���������ӿ�BC�Ƕ����ף�
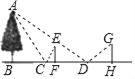
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��ƽ��ֱ������ϵxOy�У��������P�Ƶ�T��0��t����t��0����ת180��õ���Q����ô���߶�QPΪ����չ��������QΪ��P�ġ���չ�㡱��
��1����t=3ʱ������0��0���ġ���չ��������Ϊ ��������1��1��������չ�㡱����Ϊ ��
��2����� t��1������M��2��1���ġ���չ�㡱N�ں���y=��![]() ��ͼ����ʱ����t��ֵ��
��ͼ����ʱ����t��ֵ��
��3����t=1ʱ����QΪ��P��2��0���ġ���չ�㡱����������� y=��x��m��2��1�롰��չ����PQ�н��㣬��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com