
【题目】定义:在平面直角坐标系xOy中,如果将点P绕点T(0,t)(t>0)旋转180°得到点Q,那么称线段QP为“拓展带”,点Q为点P的“拓展点”.
(1)当t=3时,点(0,0)的“拓展点”坐标为 ,点(﹣1,1)的“拓展点”坐标为 ;
(2)如果 t>1,当点M(2,1)的“拓展点”N在函数y=﹣![]() 的图象上时,求t的值;
的图象上时,求t的值;
(3)当t=1时,点Q为点P(2,0)的“拓展点”,如果抛物线 y=(x﹣m)2﹣1与“拓展带”PQ有交点,求m的取值范围.
【答案】(1)(0,6),(1,5);(2)![]() ;(3)m的取值范围为
;(3)m的取值范围为![]() .
.
【解析】
(1)根据中心对称可得结果;
(2)把点M坐标带入反比例函数解析式即可得解;
(3)因为抛物线![]() 与“拓展带”PQ有交点,所以将点P、Q坐标以分别代入解析式即可解答.
与“拓展带”PQ有交点,所以将点P、Q坐标以分别代入解析式即可解答.
(1)点(0,0)的“拓展点”坐标为(0,6),点(-1,1)的“拓展点”坐标为(1,5).
(2)当t>1时,点M(2,1)的“拓展点”N为(-2,2t-1).
∵点N在函数![]() 的图象上,
的图象上,
∴![]() .
.
∴![]() .
.
(3)当t=1时,点P(2,0)的“拓展点”Q为(-2,2),
当抛物线![]() 经过点P(2,0)时,可得
经过点P(2,0)时,可得![]() 或
或![]() .
.
当抛物线![]() 经过点Q(-2,2)时,可得
经过点Q(-2,2)时,可得![]() 或
或![]() .
.
∴m的取值范围为![]() .
.


科目:初中数学 来源: 题型:
【题目】点P的“d值”定义如下:若点Q为圆上任意一点,线段PQ长度的最大值与最小值之差即为点P的“d值”,记为dP.特别的,当点P,Q重合时,线段PQ的长度为0.当⊙O的半径为2时:
(1)若点C(﹣![]() ,0),D(3,4),则dc= ,dp= ;
,0),D(3,4),则dc= ,dp= ;
(2)若在直线y=2x+2上存在点P,使得dP=2,求出点P的横坐标;
(3)直线y=﹣![]() x+b(b>0)与x轴,y轴分别交于点A,B.若线段AB上存在点P,使得2≤dP<3,请你直接写出b的取值范围.
x+b(b>0)与x轴,y轴分别交于点A,B.若线段AB上存在点P,使得2≤dP<3,请你直接写出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在暗室做小孔成像实验.如图1,固定光源(线段MN)发出的光经过小孔(动点K)成像(线段M'N')于足够长的固定挡板(直线l)上,其中MN// l.已知点K匀速运动,其运动路径由AB,BC,CD,DA,AC,BD组成.记它的运动时间为x,M'N'的长度为y,若y关于x的函数图象大致如图2所示,则点K的运动路径可能为( )
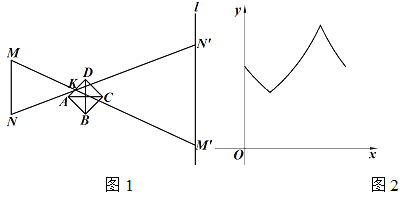
A. A→B→C→D→A B. B→C→D→A→B
C. B→C→A→D→B D. D→A→B→C→D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科幻小说《实验室的故事》中,有这样一个情节,科学家把一种珍奇的植物分别放在不同温度的环境中,经过一段时间后,记录下这种植物高度的增长情况(如下表):
温度x/℃ | … | ﹣4 | ﹣2 | 0 | 2 | 4 | 6 | … |
植物每天高度的增长量y/mm | … | 41 | 49 | 49 | 41 | 25 | 1 | … |
由这些数据,科学家推测出植物每天高度的增长量y是温度x的二次函数,那么下列三个结论:
①该植物在0℃时,每天高度的增长量最大;
②该植物在﹣6℃时,每天高度的增长量能保持在25mm左右;
③该植物与大多数植物不同,6℃以上的环境下高度几乎不增长.
上述结论中,所有正确结论的序号是
A. ①②③ B. ①③ C. ①② D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,直线L1、L2、L3,若L1与L2的距离为5,L2与L3的距离7,则正方形ABCD的面积等于( )
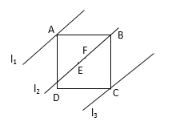
A.70B.74C.144D.148
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在(1)问的条件下,平均每天获利不变,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
(3)写出每天总利润![]() 与降价
与降价![]() 元的函数关系式,为了使每天的利润最大,应降价多少元?
元的函数关系式,为了使每天的利润最大,应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形![]() 的边长
的边长![]() .某一时刻,动点
.某一时刻,动点![]() 从
从![]() 点出发沿
点出发沿![]() 方向以
方向以![]() 的速度向
的速度向![]() 点匀速运动;同时,动点
点匀速运动;同时,动点![]() 从
从![]() 点出发沿
点出发沿![]() 方向以
方向以![]() 的速度向
的速度向![]() 点匀速运动,问:
点匀速运动,问:
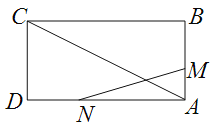
(1)经过多少时间,![]() 的面积等于矩形
的面积等于矩形![]() 面积的
面积的![]() ?
?
(2)是否存在时刻t,使以A,M,N为顶点的三角形与![]() 相似?若存在,求t的值;若不存在,请说明理由.
相似?若存在,求t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)分解因式![]() (直接写出结果);若
(直接写出结果);若![]() 是整数,则
是整数,则![]() 一定能被一个常数整除,这个常数的最大值是 .
一定能被一个常数整除,这个常数的最大值是 .
(2)阅读,并解决问题:
分解因式![]()
解:设![]() ,则原式
,则原式![]()
这样的解题方法叫做“换元法”,即当复杂的多项式中,某一部分重复出现时,我们用字母将其替换,从而简化这个多项式.换元法是一个重要的数学方法,不少问题能用换元法解决.请你用“换元法”对下列多项式进行因式分解:
①![]()
②![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
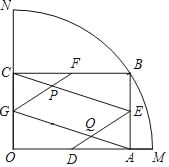
【题目】如图,扇形OMN的半径为1,圆心角为90°,点B是![]() 上一动点,BA⊥OM于点A,BC⊥ON于点C,点D、E、F、G分别是线段OA、AB、BC、CO的中点,GF与CE相交于点P,DE与AG相交于点Q.
上一动点,BA⊥OM于点A,BC⊥ON于点C,点D、E、F、G分别是线段OA、AB、BC、CO的中点,GF与CE相交于点P,DE与AG相交于点Q.
(1)当点B移动到使AB:OA=![]() :3时,求
:3时,求![]() 的长;
的长;
(2)当点B移动到使四边形EPGQ为矩形时,求AM的长.
(3)连接PQ,试说明3PQ2+OA2是定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com