
����Ŀ����ѧϰ��ԳƵ�ʱ����ʦ��ͬѧ��˼���α��е�̽���⣮
��ͼ��1����Ҫ��ȼ���ܵ�l����һ����վ���ֱ���A��B����������վ���ڹܵ���ʲô�ط�����ʹ���õ�����������̣�
�������l���Ҽ�������һ�ԣ��ܷ���ʲô���ɣ��������![]() ���Ҽ�������һ�ԣ��ܷ���ʲô���ɣ�
���Ҽ�������һ�ԣ��ܷ���ʲô���ɣ�
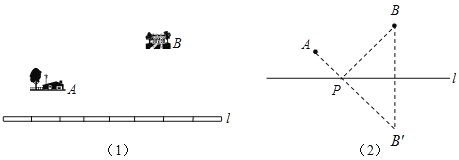
������С��ͨ������˼�����ܿ�ó��˽������������ȷ�취�����ѹܵ�l����һ��ֱ�ߣ�ͼ��2�����������ת��Ϊ��Ҫ��ֱ��l����һ��P��ʹAP��BP�ĺ���С�����������������ģ�
������B����ֱ��l�ĶԳƵ�B����
������AB����ֱ��l�ڵ�P�����PΪ����
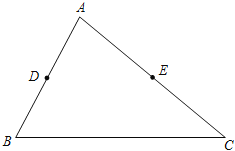
����ο�С������������������⣮��ͼ����ABC�У���D��E�ֱ���AB��AC�ߵ��е㣬BC=6��BC���ϵĸ�Ϊ4��������BC����ȷ��һ��P��ʹ��PDE���ܳ���С��
��1����ͼ��������P��������ͼ�ۼ�����д��������
��2����ֱ��д����PDE�ܳ�����Сֵ��
��
���𰸡���1����������2��8
��������
��1�������ṩ����DE���䣬ֻҪ���DP+PE����Сֵ���ɣ���D�����BC�ĶԳƵ�D��������D��E����BC���ڵ�P��P�㼴Ϊ����
��2��������λ�������Լ����ɶ����ó�D��E��ֵ�����ɵó��𰸣�
�⣺��1����D�����BC�ĶԳƵ�D��������D��E����BC���ڵ�P��P�㼴Ϊ����
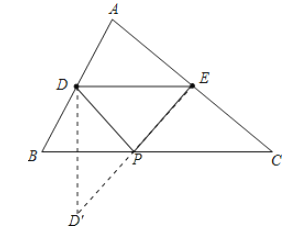
��2������D��E�ֱ���AB��AC�ߵ��е㣬
��DEΪ��ABC��λ�ߣ�
��BC=6��BC���ϵĸ�Ϊ4��
��DE=3��DD��=4��
��![]() ��
��
���PDE�ܳ�����СֵΪ��DE+D��E=3��5=8��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ����������õĿ�չ����������һ������������˽⣺����ĵ��۱�����ĵ��۶�20Ԫ����1000Ԫ��������ĸ�������800Ԫ��������ĸ�����ͬ��
��1����������ĵ��۸��Ƕ���Ԫ��
��2����ѧУ���㹺������������������100�����ҹ�����ܷ��ò�����9600Ԫ��������ܹ�����ٸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У��Խ���AC��BD���ڵ�O��DE��AB�ڵ�E������OE����DE��![]() ��BE��1�����AOE�Ķ����ǣ�������
��BE��1�����AOE�Ķ����ǣ�������
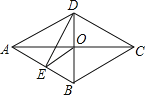
A.30��B.45��C.60��D.75��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��ͼ�٣���M��N���߶�AB�ָ��AM��MN��BN������AM��MN��BNΪ�ߵ���������һ��ֱ�������Σ���Ƶ�M��N���߶�AB�Ĺ��ɷָ�㣮
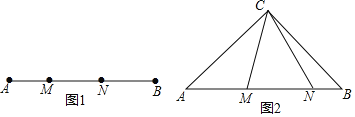
��1����֪��M��N���߶�AB�Ĺ��ɷָ�㣬��AM��2��MN��3����BN�ij���
��2����ͼ2����Rt��ABC�У�AC��BC����M��N��б��AB�ϣ���MCN��45������֤����M��N���߶�AB�Ĺ��ɷָ�㣨��ʾ������ACM�Ƶ�C��ʱ����ת90����
��3���ڣ�2����ǰ���£�����BCN��15����BN��1����AN�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ƻ�С˵��ʵ���ҵĹ��¡��У�������һ����ڣ���ѧ�Ұ�һ�������ֲ��ֱ���ڲ�ͬ�¶ȵĻ����У�����һ��ʱ���¼������ֲ��߶ȵ�������������±�����
�¶�x/�� | �� | ��4 | ��2 | 0 | 2 | 4 | 6 | �� |
ֲ��ÿ��߶ȵ�������y/mm | �� | 41 | 49 | 49 | 41 | 25 | 1 | �� |
����Щ���ݣ���ѧ���Ʋ��ֲ��ÿ��߶ȵ�������y���¶�x�Ķ��κ�������ô�����������ۣ�
�ٸ�ֲ����0��ʱ��ÿ��߶ȵ����������
�ڸ�ֲ���ک�6��ʱ��ÿ��߶ȵ��������ܱ�����25mm���ң�
�۸�ֲ��������ֲ�ﲻͬ��6�����ϵĻ����¸߶ȼ���������.
���������У�������ȷ���۵������
A. �٢ڢ� B. �٢� C. �٢� D. �ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
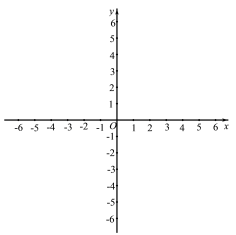
����Ŀ����ƽ��ֱ������ϵ![]() �У�������
��������![]() ������
������![]() ��
��![]() ��
��
��1���������ߵı���ʽ�Ͷ������ꣻ
��2������������A��B֮��IJ��ּ�Ϊͼ��M����A��B���㣩����ͼ��M��![]() �ᷭ�����õ�ͼ��N���������
�ᷭ�����õ�ͼ��N���������![]() ��
��![]() ��ֱ����ͼ��M��ͼ��N���ཻ����ֻ���������㣬��b��ȡֵ��Χ��
��ֱ����ͼ��M��ͼ��N���ཻ����ֻ���������㣬��b��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ɽ���ز�ר�������ۺ��ң������Ϊÿǧ��40Ԫ����ÿǧ��60Ԫ���ۣ�ƽ��ÿ����۳�100ǧ�ˣ����������г����鷢�֣�����ÿ����2Ԫ����ƽ��ÿ������ۿ�����20ǧ�ˣ�����ר�����������ֺ���Ҫ��ƽ��ÿ�����2240Ԫ����ش�
��1��ÿǧ�˺���Ӧ���۶���Ԫ��
��2������1���ʵ������£�ƽ��ÿ��������䣬Ϊ�����������ڹ˿ͣ�Ӯ���г����õ�Ӧ��ԭ�ۼ۵ļ��۳��ۣ�
��3��д��ÿ��������![]() �뽵��
�뽵��![]() Ԫ�ĺ�����ϵʽ��Ϊ��ʹÿ����������Ӧ���۶���Ԫ��
Ԫ�ĺ�����ϵʽ��Ϊ��ʹÿ����������Ӧ���۶���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��У�յ�����һ��ǽ������Ϊ20m���ó�Ϊ32m����ʺ�����ǽΧ��һ�����λ��ԣ���ͼ��ʾ��
��1����Χ�������126m2�ľ��λ��������ܣ������˵���������ܣ���˵�����ɣ�
��2�������������4m��Χ�ɵľ��λ�������ܴﵽ170m2����˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com