
【题目】校园空地上有一面墙,长度为20m,用长为32m的篱笆和这面墙围成一个矩形花圃,如图所示.
(1)能围成面积是126m2的矩形花圃吗?若能,请举例说明;若不能,请说明理由.
(2)若篱笆再增加4m,围成的矩形花圃面积能达到170m2吗?请说明理由.

【答案】(1)长为18米、宽为7米或长为14米、宽为9米;(2)若篱笆再增加4m,围成的矩形花圃面积不能达到170m2.
【解析】
(1)假设能,设AB的长度为x米,则BC的长度为(32﹣2x)米,再根据矩形面积公式列方程求解即可得到答案.
(2)假设能,设AB的长度为y米,则BC的长度为(36﹣2y)米,再根据矩形面积公式列方程,求得方程无解,即假设不成立.
(1)假设能,设AB的长度为x米,则BC的长度为(32﹣2x)米,
根据题意得:x(32﹣2x)=126,
解得:x1=7,x2=9,
∴32﹣2x=18或32﹣2x=14,
∴假设成立,即长为18米、宽为7米或长为14米、宽为9米.
(2)假设能,设AB的长度为y米,则BC的长度为(36﹣2y)米,
根据题意得:y(36﹣2y)=170,
整理得:y2﹣18y+85=0.
∵△=(﹣18)2﹣4×1×85=﹣16<0,
∴该方程无解,
∴假设不成立,即若篱笆再增加4m,围成的矩形花圃面积不能达到170m2.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:初中数学 来源: 题型:
【题目】在学习轴对称的时候,老师让同学们思考课本中的探究题.
如图(1),要在燃气管道l上修建一个泵站,分别向A、B两镇供气.泵站修在管道的什么地方,可使所用的输气管线最短?
你可以在l上找几个点试一试,能发现什么规律?你可以在![]() 上找几个点试一试,能发现什么规律?
上找几个点试一试,能发现什么规律?
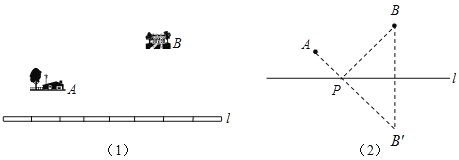
聪明的小华通过独立思考,很快得出了解决这个问题的正确办法.他把管道l看成一条直线(图(2)),问题就转化为,要在直线l上找一点P,使AP与BP的和最小.他的做法是这样的:
①作点B关于直线l的对称点B′.
②连接AB′交直线l于点P,则点P为所求.
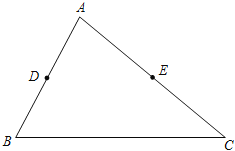
请你参考小华的做法解决下列问题.如图在△ABC中,点D、E分别是AB、AC边的中点,BC=6,BC边上的高为4,请你在BC边上确定一点P,使△PDE得周长最小.
(1)在图中作出点P(保留作图痕迹,不写作法).
(2)请直接写出△PDE周长的最小值:
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的顶点
的顶点![]() 在坐标原点,正方形
在坐标原点,正方形![]() 的边
的边![]() 与
与![]() 在同一直线上,
在同一直线上, ![]() 与
与![]() 在同一直线上,且
在同一直线上,且![]() ,
,![]() 边和
边和![]() 边所在直线的解析式分别为:
边所在直线的解析式分别为: ![]() 和
和![]() ,则点
,则点![]() 的坐标是( )
的坐标是( )
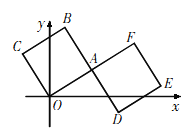
A.(6,-1)B.(7,-1)C.(7,-2)D.(6,-2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑经销商计划购进一批电脑机箱和液晶显示器,若购电脑机箱10台和液液晶显示器8台,共需要资金7000元;若购进电脑机箱2台和液示器5台,共需要资金4120元.
(1)每台电脑机箱、液晶显示器的进价各是多少元?
(2)该经销商购进这两种商品共50台,而可用于购买这两种商品的资金不超过22240元.根据市场行情,销售电脑机箱、液晶显示器一台分别可获利10元和160元.该经销商希望销售完这两种商品,所获利润不少于4100元.试问:该经销商有哪几种进货方案?哪种方案获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形组成的方格纸中,有一个以格点为顶点的△ABC.
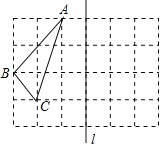
(1)△ABC的形状是 .
(2)利用网格线画△A′B′C′,使它与△ABC关于直线l对称.
(3)在直线l上求作点P使AP+CP的值最小,则AP+CP的最小值= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2016年“双十一”期间,某快递公司计划租用甲、乙两种车辆快递货物,从货物量来计算:若租用两种车辆合运,10天可以完成任务;若单独租用乙种车辆,完成任务的天数是单独租用甲种车辆完成任务天数的2倍.
(1)求甲、乙两种车辆单独完成任务分别需要多少天?
(2)已知租用甲、乙两种车辆合运需租金65000元,甲种车辆每天的租金比乙种车辆每天的租金多1500元,试问:租甲和乙两种车辆、单独租甲种车辆、单独租乙种车辆这三种租车方案中,哪一种租金最少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A,C,为半径是6的⊙O上两点,点B为![]() 的中点,以线段BA,BC为邻边作菱形ABCD,使点D落在⊙O内(不含圆周上),则下列结论:①直线BD必过圆心O;②菱形ABCD的边长a的取值范围是0<a<10;③若点D与圆心O重合,则∠ABC=120°;④若DO=2,则菱形ABCD的边长为
的中点,以线段BA,BC为邻边作菱形ABCD,使点D落在⊙O内(不含圆周上),则下列结论:①直线BD必过圆心O;②菱形ABCD的边长a的取值范围是0<a<10;③若点D与圆心O重合,则∠ABC=120°;④若DO=2,则菱形ABCD的边长为![]() 或
或![]() .其中正确的是( )
.其中正确的是( )
A. ①③ B. ②③④ C. ①③④ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com