
【题目】如图,在菱形ABCD中,对角线AC,BD交于点O,DE⊥AB于点E,连接OE,若DE=![]() ,BE=1,则∠AOE的度数是( )
,BE=1,则∠AOE的度数是( )
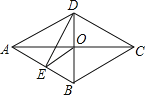
A.30°B.45°C.60°D.75°
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,已知点![]() ,点
,点![]() ,
,![]() 为线段
为线段![]() 上一点,且满足
上一点,且满足![]() .
.
(1)求直线![]() 的解析式及点
的解析式及点![]() 的坐标;
的坐标;
(2)如图2,![]() 为线段
为线段![]() 上一动点,连接
上一动点,连接![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,试探索
,试探索![]() 是否为定值?若是,求出该值;若不是,请说明理由;
是否为定值?若是,求出该值;若不是,请说明理由;
(3)点![]() 为坐标轴上一点,请直接写出满足
为坐标轴上一点,请直接写出满足![]() 为等腰三角形的所有点
为等腰三角形的所有点![]() 的坐标.
的坐标.
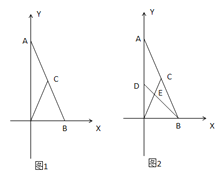
查看答案和解析>>
科目:初中数学 来源: 题型:
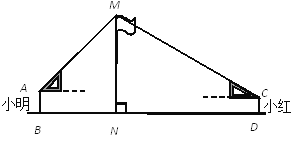
【题目】如图,在活动课上,小明和小红合作用一副三角板来测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,他调整自己的位置,设法使得三角板的一条直角边保持水平,且斜边与旗杆顶端M在同一条直线上,测得旗杆顶端M仰角为45°;小红的眼睛与地面的距离(CD)是1.5m,用同样的方法测得旗杆顶端M的仰角为30°.两人相距28米且位于旗杆两侧(点B、N、D在同一条直线上).求出旗杆MN的高度.(参考数据: ![]() ,结果保留整数.)
,结果保留整数.)
查看答案和解析>>
科目:初中数学 来源: 题型:
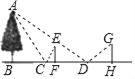
【题目】某一天,小明和小亮来到一河边,想用平面镜和皮尺测量这条河的大致宽度,两人在确保无安全隐患的情况下,现在河岸边选择了一点C(点C与河对岸岸边上的一棵树的底部点B所确定的直线垂直于河岸).小明到F点时正好在平面镜中看到树尖A,小亮在点D放置平面镜,小亮到H点时正好在平面镜中看到树尖A,且F、D、H均在BC的延长线上,小明的眼睛距地面的高度EF=1.5m,小亮的眼睛距地面的高度GH=1.6m,测得CF=1m,DH=2m,CD=8.4m,AB⊥BH,EF⊥BH,GH⊥BH,根据以上测量过程及测量数据,请你求出河宽BC是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
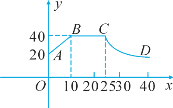
【题目】心理学家研究发现,一般情况下,在一节40分钟的课中,学生的注意力指数y随时间x(分)的变化规律如图所示(其中AB、BC为线段,CD为双曲线的一部分).
(1)分别求出线段AB和双曲线CD的函数解析式,并写出自变量的取值范围;
(2)开始上课后第5分钟时与第30分钟时比较,何时学生的注意力更集中?
(3)一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指数至少为36,那么经过适当安排,老师能否在学生达到所需的状态下讲解完这道题目?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
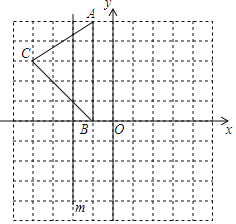
(1)在图中作出△ABC关于m(直线m上的横坐标都为﹣2)的对称图形△A1B1C1;
(2)线段上有一点P(﹣![]() ,
,![]() ),直接写出点P关于直线m对称的点的坐标 .
),直接写出点P关于直线m对称的点的坐标 .
(3)线段BC上有一点M(a,b),点M关于直线m的对称点N(c,d),请直接写出a,c的关系: ;b,d的关系: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习轴对称的时候,老师让同学们思考课本中的探究题.
如图(1),要在燃气管道l上修建一个泵站,分别向A、B两镇供气.泵站修在管道的什么地方,可使所用的输气管线最短?
你可以在l上找几个点试一试,能发现什么规律?你可以在![]() 上找几个点试一试,能发现什么规律?
上找几个点试一试,能发现什么规律?
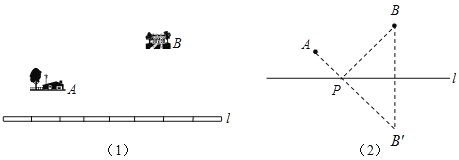
聪明的小华通过独立思考,很快得出了解决这个问题的正确办法.他把管道l看成一条直线(图(2)),问题就转化为,要在直线l上找一点P,使AP与BP的和最小.他的做法是这样的:
①作点B关于直线l的对称点B′.
②连接AB′交直线l于点P,则点P为所求.
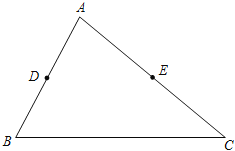
请你参考小华的做法解决下列问题.如图在△ABC中,点D、E分别是AB、AC边的中点,BC=6,BC边上的高为4,请你在BC边上确定一点P,使△PDE得周长最小.
(1)在图中作出点P(保留作图痕迹,不写作法).
(2)请直接写出△PDE周长的最小值:
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形组成的方格纸中,有一个以格点为顶点的△ABC.
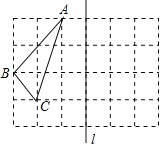
(1)△ABC的形状是 .
(2)利用网格线画△A′B′C′,使它与△ABC关于直线l对称.
(3)在直线l上求作点P使AP+CP的值最小,则AP+CP的最小值= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com