
【题目】心理学家研究发现,一般情况下,在一节40分钟的课中,学生的注意力指数y随时间x(分)的变化规律如图所示(其中AB、BC为线段,CD为双曲线的一部分).
(1)分别求出线段AB和双曲线CD的函数解析式,并写出自变量的取值范围;
(2)开始上课后第5分钟时与第30分钟时比较,何时学生的注意力更集中?
(3)一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指数至少为36,那么经过适当安排,老师能否在学生达到所需的状态下讲解完这道题目?说明理由.
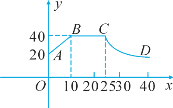
【答案】(1)线段AB所在的直线的解析式为y1=2x+20.(0≤x≤10),CD所在双曲线的解析式为y2=![]() (25≤x≤40);(2)第30分钟注意力更集中.(3)经过适当安排,老师能在学生注意力达到所需的状态下讲解完这道题目.
(25≤x≤40);(2)第30分钟注意力更集中.(3)经过适当安排,老师能在学生注意力达到所需的状态下讲解完这道题目.
【解析】
(1)用待定系数法分别求出AB和CD的函数表达式即可;
(2)分别求第5分钟和第30分钟的注意力指数,最后比较判断;
(3)分别求出注意力指数为36时的两个时间,再将两时间之差和19比较,大于19则能讲完,否则不能.
解:(1)设线段AB所在的直线的解析式为y1=k1x+20,
把B(10,40)代入得,k1=2,
∴y1=2x+20.(0≤x≤10)
设C、D所在双曲线的解析式为y2=![]() ,
,
把C(25,40)代入得,k2=1000,
∴y2=![]() (25≤x≤40);
(25≤x≤40);
(2)当x1=5时,y1=2×5+20=30,
当 x1=30时,y2=![]() =
=![]() ,
,
∴y1<y2,
∴第30分钟注意力更集中.
(3)令y1=36,
∴36=2x+20,
∴x1=8,
令y2=36,
∴36=![]() ,
,
∴x2=![]() ≈27.8;
≈27.8;
∵27.8-8=19.8>19,
∴经过适当安排,老师能在学生注意力达到所需的状态下讲解完这道题目.


 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
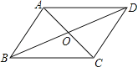
A.AB∥CD,AD∥BCB.OA=OC,OB=OD
C.AD=BC,AB∥CDD.AB=CD,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,任取一点O,连AO,BO,CO,分别取点D,E,F,使OD=![]() AO,OE=
AO,OE=![]() BO,OF=
BO,OF=![]() CO,得△DEF,有下列说法:
CO,得△DEF,有下列说法:
①△ABC与△DEF是位似图形;②△ABC与△DEF是相似图形;
③△DEF与△ABC的周长比为1:3;④△DEF与△ABC的面积比为1:6.
则正确的个数是( )
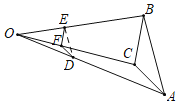
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC,BD交于点O,DE⊥AB于点E,连接OE,若DE=![]() ,BE=1,则∠AOE的度数是( )
,BE=1,则∠AOE的度数是( )
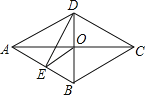
A.30°B.45°C.60°D.75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,AC=BC,点D是△ABC内一点,若AC=AD,∠CAD=30°,连接BD,则∠ADB的度数为( )
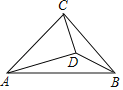
A.120°B.135°C.150°D.165°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图①,点M、N把线段AB分割成AM、MN和BN,若以AM,MN、BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.
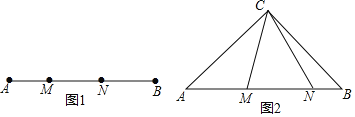
(1)已知点M、N是线段AB的勾股分割点,若AM=2,MN=3,求BN的长;
(2)如图2,在Rt△ABC中,AC=BC,点M,N在斜边AB上,∠MCN=45°,求证:点M,N是线段AB的勾股分割点(提示:把△ACM绕点C逆时针旋转90°)
(3)在(2)的前提下,若∠BCN=15°,BN=1.求AN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 经过点
经过点![]() 和
和![]() .
.
(1)求抛物线的表达式和顶点坐标;
(2)将抛物线在A、B之间的部分记为图象M(含A、B两点).将图象M沿![]() 轴翻折,得到图象N.如果过点
轴翻折,得到图象N.如果过点![]() 和
和![]() 的直线与图象M、图象N都相交,且只有两个交点,求b的取值范围.
的直线与图象M、图象N都相交,且只有两个交点,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AB=AC,在△ABC的外侧作直线AP,点C关于直线AP的对称点为点D,连接AD,BD,其中BD交直线AP于点E.
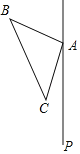
(1)依题意补全图形;
(2)若∠PAC=24°,求∠AEB的度数;
(3)连结CE,若AE=![]() ,CE=1,求BE长.
,CE=1,求BE长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com