练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

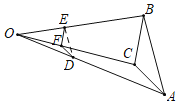
    【题目】如图，已知△ABC，任取一点O，连AO，BO，CO，分别取点D，E，F，使OD＝AO，OE＝BO，OF＝CO，得△DEF，有下列说法：

    ①△ABC与△DEF是位似图形；②△ABC与△DEF是相似图形；

    ③△DEF与△ABC的周长比为1：3；④△DEF与△ABC的面积比为1：6．

    则正确的个数是（　　）

    A.1B.2C.3D.4

    【答案】C

    【解析】

    直接利用位似图形的性质以及相似图形的性质分别分析得出答案．

    解：∵任取一点O，连AO，BO，CO，分别取点D，E，F，OD＝AO，OE＝BO，OF＝CO，

    ∴△DEF与△ABC的相似比为：1：3，

    ∴①△ABC与△DEF是位似图形，正确；

    ②△ABC与△DEF是相似图形，正确；

    ③△DEF与△ABC的周长比为1：3，正确；

    ④△DEF与△ABC的面积比为1：9，故此选项错误．

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】金堂县在创建国家卫生城市的过程中，经调查发现居民用水量居高不下，为了鼓励居民节约用水，拟实行新的收费标准．若每月用水量不超过12吨，则每吨按政府补贴优惠价元收费；若每月用水量超过12吨，则超过部分每吨按市场指导价元收费．毛毛家家10月份用水22吨，交水费59元；11月份用水17吨，交水费41．5元．

    （1）求每吨水的政府补贴优惠价和市场指导价分别是多少元？

    （2）设每月用水量为吨，应交水费为元，请写出与之间的函数关系式；

    （3）小明家12月份用水25吨，则他家应交水费多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在矩形中，点为边中点，点为边中点；点， 为边三等分点， ， 为边三等分点.小瑞分别用不同的方式连接矩形对边上的点，如图2，图3所示.那么，图2中四边形的面积与图3中四边形的面积相等吗？

    （1）小瑞的探究过程如下

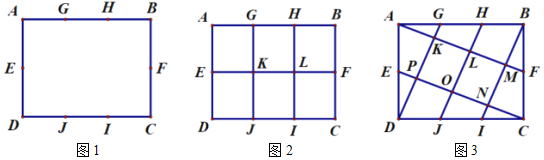
    在图2中，小瑞发现， ；

    在图3中，小瑞对四边形面积的探究如下. 请你将小瑞的思路填写完整：

    设，

    ∵

    ∴，且相似比为，得到

    ∵

    ∴，且相似比为，得到

    又∵，

    ∴

    ∴， ，

    ∴，则（填写“”，“”或“”）

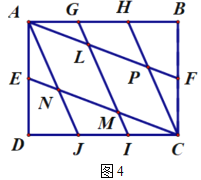
    （2）小瑞又按照图4的方式连接矩形对边上的点.则.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

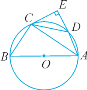
    【题目】如图所示，△ABC内接于⊙O，AB是⊙O的直径，点D在⊙O上，连接CD且DC=BC，过C点作AD的垂线交AD延长线于E.

    （1）求证：CE是⊙O的切线；

    （2）若AB=5，AC=4，求tan∠DCE的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，，，垂足分别为E、D，CE，BD相交于．

    （1）若，求证：；

    （2）若，求证：．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某工厂计划生产甲、乙两种产品共2500吨，每生产1吨甲产品可获得利润0.3万元，每生产1吨乙产品可获得利润0.4万元．设该工厂生产了甲产品x（吨），生产甲、乙两种产品获得的总利润为y（万元）．

    （1）求y与x之间的函数表达式；

    （2）若每生产1吨甲产品需要A原料0.25吨，每生产1吨乙产品需要A原料0.5吨．受市场影响，该厂能获得的A原料至多为1000吨，其它原料充足．求出该工厂生产甲、乙两种产品各为多少吨时，能获得最大利润．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

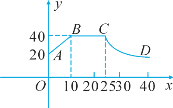
    【题目】心理学家研究发现，一般情况下，在一节40分钟的课中，学生的注意力指数y随时间x（分）的变化规律如图所示（其中AB、BC为线段,CD为双曲线的一部分）.

    （1）分别求出线段AB和双曲线CD的函数解析式，并写出自变量的取值范围；

    （2）开始上课后第5分钟时与第30分钟时比较，何时学生的注意力更集中？

    （3）一道数学竞赛题，需要讲19分钟，为了效果较好，要求学生的注意力指数至少为36，那么经过适当安排，老师能否在学生达到所需的状态下讲解完这道题目？说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，C、E和B、D、F分别在∠GAH的两边上，且AB=BC=CD=DE=EF，若∠A=18°，则∠GEF的度数是（ ）

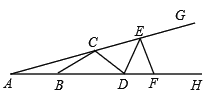
    A. 80° B. 90° C. 100° D. 108°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某电脑经销商计划购进一批电脑机箱和液晶显示器，若购电脑机箱10台和液液晶显示器8台，共需要资金7000元；若购进电脑机箱2台和液示器5台，共需要资金4120元．

    （1）每台电脑机箱、液晶显示器的进价各是多少元？

    （2）该经销商购进这两种商品共50台，而可用于购买这两种商品的资金不超过22240元．根据市场行情，销售电脑机箱、液晶显示器一台分别可获利10元和160元．该经销商希望销售完这两种商品，所获利润不少于4100元．试问：该经销商有哪几种进货方案？哪种方案获利最大？最大利润是多少？

    查看答案和解析>>

    同步练习册答案