
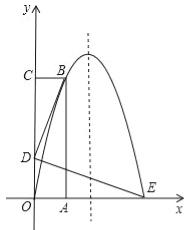
����Ŀ����ͼ��������OABC��OA����x����������ϣ�OC��y����������ϣ�������y=ax2+bx������B��1��4���͵�E��3��0�����㣮
��1���������ߵĽ���ʽ��
��2������D���߶�OC�ϣ���BD��DE��BD=DE����D������ꣻ
��3����������2���£��������ߵĶԳ�������һ��M��ʹ�á�BDM���ܳ�Ϊ��С�������BDM�ܳ�����Сֵ����ʱ��M�����ꣻ
��4����������2���£���B�㵽E����������ߵ�ͼ���ϣ��Ƿ����һ����P��ʹ�á�PAD�������������ڣ��������PAD��������ֵ����ʱP������ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y=��2x2+6x����2��D��0��1������3����BDM���ܳ���СֵΪ![]() ��M��
��M��![]() ��
��![]() ������4����P��������
������4����P��������![]() ��
��![]() ����
����
��������
�����������1������B��1��4����E��3��0����������������ߵĽ���ʽ���õ�����a��b�ķ����飬���a��b��ֵ���Ӷ��ɵõ������ߵĽ���ʽ����2������ͬ�ǵ�������֤����BDC=��DE0��Ȼ��������AAS֤����BDC�ա�DEO���Ӷ��õ�OD=AO=1�����ǿ���õ�D�����ꣻ��3������B���������ߵĶԳ���ĶԳƵ�B��������B��D�������ߵĶԳ������M������������ߵĶԳ��᷽�̣��Ӷ��õ���B�������꣬����ԳƵ����ʿ�֪����D��M��B����һ��ֱ����ʱ����BMD���ܳ�����Сֵ�����������ľ��빫ʽ���BD��B��D�ij��ȣ��Ӷ��õ������ε��ܳ���Сֵ��Ȼ�����ݴ���ϵ�������D��B���Ľ���ʽ��Ȼ��M�ĺ�����������õ�M�������ꣻ��4������F��FG��x�ᣬ����ΪG�����F��a����2a2+6a������OG=a��FG=��2a2+6a��Ȼ������S��FDA=S����DOGF��S��ODA��S��AGF�������ε������a�ĺ�����ϵʽ��Ȼ�����ݶ��κ�����������⼴�ɣ�
�����������1������B��1��4����E��3��0����������������ߵĽ���ʽ�ã�![]() ��
��
��ã�a=-2��b=6��
�����ߵĽ���ʽΪy=��2x2+6x��
��2����ͼ1��ʾ��
��BD��DE��
���BDE=90����
���BDC+��EDO=90����
���ߡ�ODE+��DEO=90����
���BDC=��DE0��
����BDC����DOE��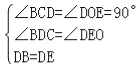 ��
��
���BDC�ա�DEO��
��OD=AO=1��
��D��0��1����
��3����ͼ2��ʾ������B���������ߵĶԳ���ĶԳƵ�B��������B��D�������ߵĶԳ������M��
��x=��![]() =
=![]() ��
��
����B����������2��4����
����B���B������x=![]() �Գƣ�
�Գƣ�
��MB=B��M��
��DM+MB=DM+MB����
������D��M��B����һ��ֱ����ʱ��MD+MB����Сֵ������BMD���ܳ�����Сֵ����
���������ľ��빫ʽ��֪��BD=![]() ��DB��=
��DB��=![]() ��
��
���BDM����Сֵ=![]() ��
��
��ֱ��B��D�Ľ���ʽΪy=kx+b��
����D��B�����������ã�![]() ��
��
��ã�k=![]() ��b=1��
��b=1��
��ֱ��DB���Ľ���ʽΪy=![]() x+1��
x+1��
��x=![]() ����ã�y=
����ã�y=![]() ��
��
��M��![]() ��
��![]() ����
����
��4����ͼ3��ʾ������F��FG��x�ᣬ����ΪG��
���F��a����2a2+6a������OG=a��FG=��2a2+6a��
��S����DOGF=![]() ��OD+FG��OG=
��OD+FG��OG=![]() ����2a2+6a+1����a=��a3+3a2+
����2a2+6a+1����a=��a3+3a2+![]() a��S��ODA=
a��S��ODA=![]() ODOA=
ODOA=![]() ��1��1=
��1��1=![]() ��S��AGF=
��S��AGF=![]() AGFG=��a3+4a2��3a��
AGFG=��a3+4a2��3a��
��S��FDA=S����DOGF��S��ODA��S��AGF=��a2+![]() a��
a��![]() ��
��
����a=![]() ʱ��S��FDA�����ֵΪ
ʱ��S��FDA�����ֵΪ![]() ��
��
����P��������![]() ��
��![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2x2��2y2����3��x2y2+x2��+3��x2y2+y2��������x=��1��y=2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����䷽���ⷽ��x2��2x��5=0ʱ��ԭ����Ӧ����Ϊ�� ��
A.��x+1��2=6
B.��x+2��2=9
C.��x��1��2=6
D.��x��2��2=9
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������A��B��ʾ�����ֱ�Ϊ��3��1����PΪ����������һ�㣬���ʾ����Ϊx�������P����A����B�ľ���֮��Ϊ6����x��ֵ�ǣ�������
A. ��4 B. 2 C. 4 D. ��4��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���÷�֤��֤�����ı�����������һ�����Ƕ۽ǻ�ֱ������Ӧ�ȼ��裨 ��
A.ÿһ���Ƕ��Ƕ۽ǻ�ֱ��B.���������Ƕ۽ǻ�ֱ��
C.û��һ�����Ƕ۽ǻ�ֱ��D.���������������ϵĽ��Ƕ۽ǻ�ֱ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
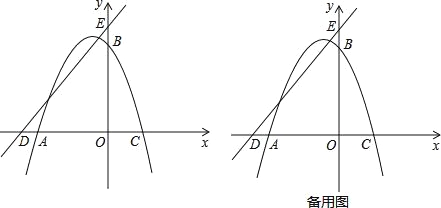
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬������y=ax2+2xa+c����A����4��0����B��0��4�����㣬��x�ύ����һ��C��ֱ��y=x+5��x�ύ�ڵ�D����y�ύ�ڵ�E��
��1���������ߵĽ���ʽ��
��2����P�ǵڶ������������ϵ�һ�����㣬����EP������E��EP�Ĵ���l����l�Ͻ�ȡ�߶�EF��ʹEF=EP���ҵ�F�ڵ�һ���ޣ�����F��FM��x���ڵ�M�����P�ĺ�����Ϊt���߶�FM�ij���Ϊd����d��t֮��ĺ�����ϵʽ����Ҫ��д���Ա���t��ȡֵ��Χ����
��3���ڣ�2���������£�����E��EH��ED��MF���ӳ����ڵ�H������DH����GΪDH���е㣬��ֱ��PG����AC���е�Qʱ�����F�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABC�У���B =��C��BD=CF��BE=CD����EDF=���������н�����ȷ���ǣ� ��
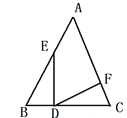
A. 2��+��A=90�� B. 2��+��A=180��
C. ��+��A=90�� D. ��+��A=180��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ʽ��ȷ���ǣ�������
A. ����14����5=��9 B. |6��3|=����6��3��
C. ����3��������3��=��6 D. 0������4��=4
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com