
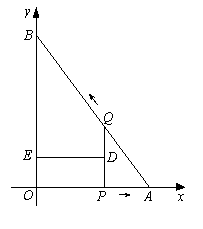
如图,在平面直角坐标系xOy中,直线AB与x轴交于点A, 与y轴交于点B, 且OA = 3,AB = 5.点P从点O出发沿OA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AO返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BO-OP于点E.点P、Q同时出发,当点Q到达点B时停止运动,点P也随之停止.设点P、Q运动的时间是t秒(t>0).
(1)求直线AB的解析式;
(2)在点P从O向A运动的过程中,求△APQ的面积S与t之间的函数关系式(不必写出t的取值范围);
(3)在点E从B向O运动的过程中,完成下面问题:
①四边形QBED能否成为直角梯形?若能,请求出t的值;若不能,请说明理由;
②当DE经过点O时,请你直接写出t的值.
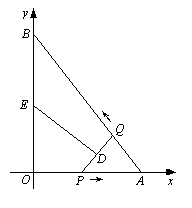
解:解:(1)在Rt△AOB中,OA = 3,AB = 5,由勾股定理得![]() .
.
∴A(3,0),B(0,4).
 设直线AB的解析式为
设直线AB的解析式为![]() .
.
∴![]() 解得
解得 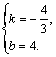
∴直线AB的解析式为![]()
| |
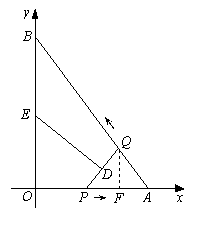
∵ AQ = OP= t,∴![]() .
.
由△AQF∽△ABO,得![]() .
.
 ∴
∴![]() .∴
.∴![]() .
.
∴![]() ,
,
∴![]() .
.
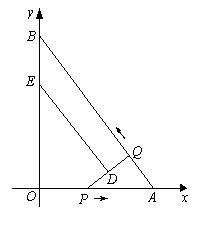
(3)四边形QBED能成为直角梯形.
①如图,当DE∥QB时,
∵DE⊥PQ,
![]() ∴PQ⊥QB,四边形QBED是直角梯形.
∴PQ⊥QB,四边形QBED是直角梯形.
此时∠AQP=90°.
由△APQ ∽△ABO,得![]() .
.
∴![]() .
.
 解得
解得![]() .
.
②如图,当PQ∥BO时,
∵DE⊥PQ,
∴DE⊥BO,四边形QBED是直角梯形.
此时∠APQ =90°.
由△AQP ∽△ABO,得 ![]()
即![]() .
.
解得![]() .
.
(4)![]() 或
或![]() .
.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案科目:初中数学 来源: 题型:
 如图,在平面直角坐标中,四边形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,点P为x轴上的一个动点,但是点P不与点0、点A重合.连接CP,D点是线段AB上一点,连接PD.
如图,在平面直角坐标中,四边形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,点P为x轴上的一个动点,但是点P不与点0、点A重合.连接CP,D点是线段AB上一点,连接PD.| BD |
| AB |
| 5 |
| 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•渝北区一模)如图,在平面直角坐标xoy中,以坐标原点O为圆心,3为半径画圆,从此圆内(包括边界)的所有整数点(横、纵坐标均为整数)中任意选取一个点,其横、纵坐标之和为0的概率是
(2012•渝北区一模)如图,在平面直角坐标xoy中,以坐标原点O为圆心,3为半径画圆,从此圆内(包括边界)的所有整数点(横、纵坐标均为整数)中任意选取一个点,其横、纵坐标之和为0的概率是| 5 |
| 29 |
| 5 |
| 29 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数y=
如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数y=| k |
| x |
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 ∠COA=45°,动点P从点O出发,在梯形OABC的边上运动,路径为O→A→B→C,到达点C时停止.作直线CP.
∠COA=45°,动点P从点O出发,在梯形OABC的边上运动,路径为O→A→B→C,到达点C时停止.作直线CP.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com