
【题目】如图,以![]() 边为直径的⊙
边为直径的⊙![]() 经过点
经过点![]() ,
,![]() 是⊙
是⊙![]() 上一点,连结
上一点,连结![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,
,![]() .
.
(1)试判断![]() 与⊙
与⊙![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若点![]() 是弧
是弧![]() 的中点,已知
的中点,已知![]() ,求
,求![]() 的值.
的值.

【答案】(1)![]() 是⊙
是⊙![]() 的切线.证明见解析;(2)8.
的切线.证明见解析;(2)8.
【解析】
试题(1)连结OP,根据圆周角定理可得∠AOP=2∠ACP=120°,然后计算出∠PAD和∠D的度数,进而可得∠OPD=90°,从而证明PD是⊙O的切线;
(2)连结BC,首先求出∠CAB=∠ABC=∠APC=45°,然后可得AC长,再证明△CAE∽△CPA,进而可得![]() ,然后可得CECP的值.
,然后可得CECP的值.
试题解析:(1)如图,![]() 是⊙
是⊙![]() 的切线.证明如下:
的切线.证明如下:
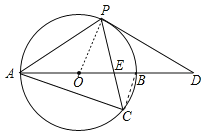
连结OP,
∵∠ACP=60°,
∴∠AOP=120°,
∵OA=OP,
∴∠OAP=∠OPA=30°,
∵PA=PD,
∴∠PAO=∠D=30°,
∴∠OPD=90°,
∴PD是⊙O的切线.
(2)连结BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
又∵C为弧AB的中点,
∴∠CAB=∠ABC=∠APC=45°,
∵AB=4,AC=ABsin45°=2![]() .
.
∵∠C=∠C,∠CAB=∠APC,
∴△CAE∽△CPA,
∴![]() ,
,
∴CPCE=CA2=(2![]() )2=8.
)2=8.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】中秋节前夕,某公司的李会计受公司委派去超市购买若干盒美心月饼,超市给出了该种月饼不同购买数量的价格优惠,如图,折线ABCD表示购买这种月饼每盒的价格y(元)与盒数x(盒)之间的函数关系.
(1)当购买这种月饼盒数不超过10盒时,一盒月饼的价格为 元;
(2)求出当10<x<25时,y与x之间的函数关系式;
(3)当时李会计支付了3600元购买这种月饼,那么李会计买了多少盒这种月饼?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地城管需要从甲、乙两个仓库向A、B两地分别运送10吨和5吨的防寒物资,甲、乙两仓库分别有8吨、7吨防寒物资.从甲、乙两仓库运送防寒物资到A、B两地的运费单价(元/吨)如表1,设从甲仓库运送到A地的防寒物资为x吨(如表2).
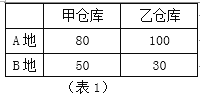

(1)完成表2 , ;
(2)求运送的总运费y(元)与x(吨)之间的函数表达式,并直接写出x的取值范围;
(3)直接写出最低总运费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 ![]() 中,
中,![]() ,F是 AB 延长线上一点,
,F是 AB 延长线上一点,![]() ,
,![]() 于点 D,交 BC 于点E.
于点 D,交 BC 于点E.
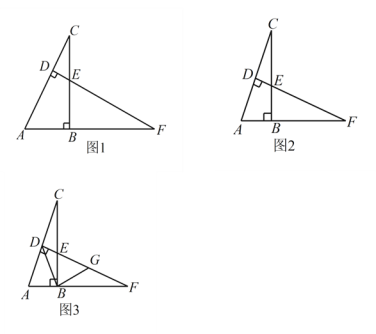
(1)如图1,求证:![]() ;
;
(2)如图2,若点 ![]() 是
是 ![]() 边的中点,求
边的中点,求 ![]() 的度数;
的度数;
(3)如图3,在(2)的条件下,连接 ![]() ,作
,作 ![]() ,交
,交 ![]() 于点G,若
于点G,若 ![]() ,
,![]() .求
.求 ![]() 的面积
的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学在百货商场购进了A、B两种品牌的篮球,购买A品牌蓝球花费了2400元,购买B品牌蓝球花费了1950元,且购买A品牌蓝球数量是购买B品牌蓝球数量的2倍,已知购买一个B品牌蓝球比购买一个A品牌蓝球多花50元.
(1)求购买一个A品牌、一个B品牌的蓝球各需多少元?
(2)该学校决定再次购进A、B两种品牌蓝球共30个,恰逢百货商场对两种品牌蓝球的售价进行调整,A品牌蓝球售价比第一次购买时提高了10%,B品牌蓝球按第一次购买时售价的9折出售,如果这所中学此次购买A、B两种品牌蓝球的总费用不超过3200元,那么该学校此次最多可购买多少个B品牌蓝球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=EC.求证:

(1)△ABC≌△DEF;
(2)FG=CG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市在2017年“双11”,销售一批用16800元购进的中老年人保暖内衣,发现供不应求.为了备战“双12”,积极参与支付宝扫码领红包活动,超市又用36400元购进了第二批这种保暖内衣,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该超市购进的第一批保暖内衣是多少件?
(2)两批保暖内衣按相同的标价销售,最后剩下的50件按六折优惠卖出,两批保暖内衣全部售完后利润没有低于进价的20%(不考虑其他因素),请计算每件保暖内衣的标价至少是多少元?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com