
【题目】如图,在 ![]() 中,
中,![]() ,F是 AB 延长线上一点,
,F是 AB 延长线上一点,![]() ,
,![]() 于点 D,交 BC 于点E.
于点 D,交 BC 于点E.
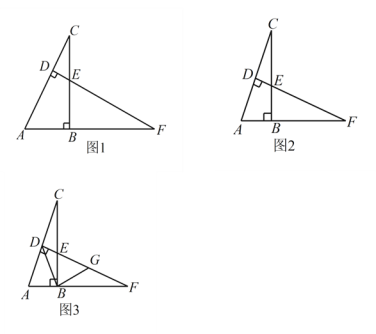
(1)如图1,求证:![]() ;
;
(2)如图2,若点 ![]() 是
是 ![]() 边的中点,求
边的中点,求 ![]() 的度数;
的度数;
(3)如图3,在(2)的条件下,连接 ![]() ,作
,作 ![]() ,交
,交 ![]() 于点G,若
于点G,若 ![]() ,
,![]() .求
.求 ![]() 的面积
的面积
【答案】(1)详见解析;(2)67.5°;(3)![]() .
.
【解析】
(1)先证明三角形全等,利用全等性质即可解出此题
(2)连接CF,得出等腰Rt△BCF,由此得出角度关系,根据D又是中点DF⊥AC可以得出△AFC为等腰三角形,则DF就为角平分线,因此可以得出角度关系,联合求解即可.
(3)先证出△BCD≌△BFG,再证出△ABC≌△EBF,从而得出BEG和BEF的关系即可.
(1)证明:
∵FD⊥AC
∴∠ADF=90°
∵∠ABC=90°
∴∠ADF=∠ABC=∠EBF
∵∠C+∠A=∠F+∠A=90°
∴∠C=∠F
在△ABC和△EBF中
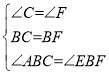
∴△ABC≌△EBF
∴AC=EF
(2)
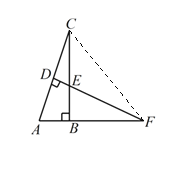
连接CF
∵点D是AC中点
∴AD=CD
∵FD⊥AC
∴∠ADF=∠CDF=90°
在△ADF和△CDF中
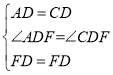
∴△ADF≌△CDF
∴∠AFD=∠CFD
∵BF=BC,BC⊥BF
∴△BCF是等腰直角三角形
∴∠BFC=∠BCF=∠AFD+∠CFD=45°
∴∠AFD=∠CFD=22.5°
∴∠A=90°-∠AFD=90°-22.5°=67.5°
(3)∵BG⊥BD
∴∠DBG=90°
∴∠DBC+∠EBG=∠FBG+∠EBG=90°
∴∠DBC=∠FBG
在△BCD和△BFG中
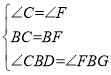
∴△BCD≌△BFG
∴CD=FG
∵CD=AD,AC=EF
∴FG=EG
∵△ABC≌△EBF
∴AB=BE=1
∴BF=BC=BE+CE=1+![]()
∴![]()


科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(﹣![]() ,0),点B的坐标为(0,3).
,0),点B的坐标为(0,3).
(1)求过A,B两点直线的函数表达式;
(2)过B点作直线BP与x轴交于点P,且使OP=2OA,求△ABP的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知等腰直角![]() 中,BD为斜边上的中线,E为DC上的一点,且
中,BD为斜边上的中线,E为DC上的一点,且![]() 于G,AG交BD于F.
于G,AG交BD于F.
(1)求证:AF=BE.
(2)如图②,当点E在DC的延长线上,其它条件不变,①的结论还能成立吗?若不能,请说明理由;若能,请予以证明。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在求1+3+32+34+35+36+37+38的值时,张红发现:从第二个加数起每一个加数都是前一个加数的3倍,于是她假设:S=1+3+32+33+34+35+36+37+38①,然后在①式的两边都乘以3,得:3S=3+32+33+34+35+36+37+38+39②,②﹣①得:3S﹣S=39﹣1,即2S=39﹣1,∴S=![]() .
.
请阅读张红发现的规律,并帮张红解决下列问题:
(1)爱动脑筋的张红想:如果把“3”换成字母m(m≠0且m≠1),应该能用类比的方法求出1+m+m2+m3+m4+…+m2018的值,对该式的值,你的猜想是______(用含m的代数式表示).
(2)证明你的猜想是正确的.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,直线L:y=mx+5m与x轴负半轴,y轴正半轴分别交于A、B两点.
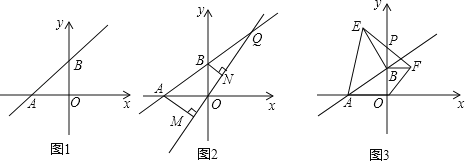
(1)当OA=OB时,求点A坐标及直线L的解析式;
(2)在(1)的条件下,如图②所示,设Q为AB延长线上一点,作直线OQ,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM=4,求BN的长;
(3)当m取不同的值时,点B在y轴正半轴上运动,分别以OB、AB为边,点B为直角顶点在第一、二象限内作等腰直角△OBF和等腰直角△ABE,连EF交y轴于P点,如图③.
问:当点B在y轴正半轴上运动时,试猜想PB的长是否为定值?若是,请求出其值;若不是,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
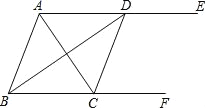
【题目】如图,AE∥BF,AC平分∠BAE,交BF于点C,BD平分∠ABC,交AE于点D,连接CD.
(1)求证:四边形ABCD是菱形;
(2)若AB=5,AC=6,求AE,BF之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC,将其绕点A逆时针旋转15°得到Rt△AB′C′,B′C′交AB于E,若图中阴影部分面积为![]() ,则B′E的长为__.
,则B′E的长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 如图
如图![]() ,
,![]() 中,
中,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,在
,在![]() 上截取
上截取![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .求证:四边形
.求证:四边形![]() 是菱形;
是菱形;
![]() 如图
如图![]() ,
,![]() 中,
中,![]() 平分
平分![]() 的外角
的外角![]() 交
交![]() 的延长线于点
的延长线于点![]() ,在
,在![]() 的延长线上截取
的延长线上截取![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .四边形
.四边形![]() 还是菱形吗?如果是,请证明;如果不是,请说明理由.
还是菱形吗?如果是,请证明;如果不是,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com