
【题目】在求1+3+32+34+35+36+37+38的值时,张红发现:从第二个加数起每一个加数都是前一个加数的3倍,于是她假设:S=1+3+32+33+34+35+36+37+38①,然后在①式的两边都乘以3,得:3S=3+32+33+34+35+36+37+38+39②,②﹣①得:3S﹣S=39﹣1,即2S=39﹣1,∴S=![]() .
.
请阅读张红发现的规律,并帮张红解决下列问题:
(1)爱动脑筋的张红想:如果把“3”换成字母m(m≠0且m≠1),应该能用类比的方法求出1+m+m2+m3+m4+…+m2018的值,对该式的值,你的猜想是______(用含m的代数式表示).
(2)证明你的猜想是正确的.
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,AB=m,BC=6,点P为线段AD上任一点
(1)若∠BPC=60°,请在图中用尺规作图画出符合要求的点P;(保留作图痕迹,不要求写作法)
(2)若符合(1)中要求的点P必定存在,求m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A城出发沿一条笔直公路匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离![]() (千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.
(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.
(1)A,B两城相距 千米,乙车比甲车早到 小时;
(2)甲车出发多长时间与乙车相遇?
(3)若两车相距不超过20千米时可以通过无线电相互通话,则两车都在行驶过程中可以通过无线电通话的时间有多长?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:
数学活动课上,李老师给出如下定义:如果一个三角形有一边上的中线等于这条边的一半,那么称三角形为“智慧三角形”.

理解:
⑴如图![]() ,已知
,已知![]() 是⊙
是⊙![]() 上两点,请在圆上找出满足条件的点
上两点,请在圆上找出满足条件的点![]() ,使
,使![]() 为“智慧三角形”(画出点
为“智慧三角形”(画出点![]() 的位置,保留作图痕迹);
的位置,保留作图痕迹);
⑵如图![]() ,在正方形
,在正方形![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 上一点,且
上一点,且![]() ,试判断
,试判断![]() 是否为“智慧三角形”,并说明理由;
是否为“智慧三角形”,并说明理由;
运用:
⑶如图![]() ,在平面直角坐标系
,在平面直角坐标系![]() 中,⊙
中,⊙![]() 的半径为
的半径为![]() ,点
,点![]() 是直线
是直线![]() 上的一点,若在⊙
上的一点,若在⊙![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 为“智慧三角形”,当其面积取得最小值时,直接写出此时点
为“智慧三角形”,当其面积取得最小值时,直接写出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地城管需要从甲、乙两个仓库向A、B两地分别运送10吨和5吨的防寒物资,甲、乙两仓库分别有8吨、7吨防寒物资.从甲、乙两仓库运送防寒物资到A、B两地的运费单价(元/吨)如表1,设从甲仓库运送到A地的防寒物资为x吨(如表2).
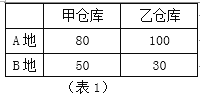

(1)完成表2 , ;
(2)求运送的总运费y(元)与x(吨)之间的函数表达式,并直接写出x的取值范围;
(3)直接写出最低总运费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是菱形
是菱形![]() 的对角线
的对角线![]() 、
、![]() 的交点,
的交点,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点.下列结论:①
的中点.下列结论:①![]() ;②四边形
;②四边形![]() 也是菱形;③四边形
也是菱形;③四边形![]() 的面积为
的面积为![]() ;④
;④![]() ;⑤
;⑤![]() 是轴对称图形.其中正确的结论有( )
是轴对称图形.其中正确的结论有( )

A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 ![]() 中,
中,![]() ,F是 AB 延长线上一点,
,F是 AB 延长线上一点,![]() ,
,![]() 于点 D,交 BC 于点E.
于点 D,交 BC 于点E.
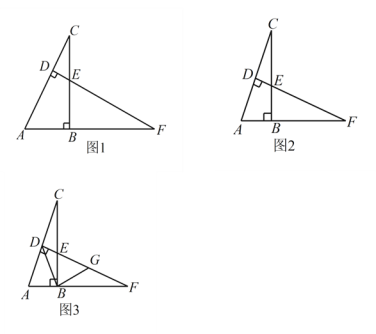
(1)如图1,求证:![]() ;
;
(2)如图2,若点 ![]() 是
是 ![]() 边的中点,求
边的中点,求 ![]() 的度数;
的度数;
(3)如图3,在(2)的条件下,连接 ![]() ,作
,作 ![]() ,交
,交 ![]() 于点G,若
于点G,若 ![]() ,
,![]() .求
.求 ![]() 的面积
的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=EC.求证:

(1)△ABC≌△DEF;
(2)FG=CG.
查看答案和解析>>
科目:初中数学 来源: 题型:
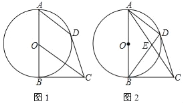
【题目】如图1,AB是⊙O的直径,BC是⊙O的切线,OC∥弦AD
(1)求证:CD是⊙O的切线;
(2)如图2,连AC交BD于E.若AE=CE,求tan∠ACB的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com