Question

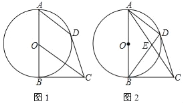
【题目】如图1，AB是⊙O的直径，BC是⊙O的切线，OC∥弦AD

（1）求证：CD是⊙O的切线；

（2）如图2，连AC交BD于E．若AE=CE，求tan∠ACB的值．

Answer 1

【答案】(1)见解析;(2).

【解析】

（1）欲证明CD是⊙O的切线，只要证明∠ODC=90°，只要证明△OCD≌△OCB即可．

（2）如图2中，连接OC交BD于点M，连接OE，设EM=a，BM=2a，利用△EOM∽△EBO，得EO2=EMEB，求出EO、EB即可解决问题．

（1）证明：如图1中，连接BD、OD，BD与OC交于点E．

∵AB是直径，

∴∠ADB=90°，

∴AD⊥BD，

∵AD∥OC，

∴OC⊥BD，ED=BE，

∵OD=OB，

∴∠DOC=∠BOC，

∵BC是⊙O切线，

∴OB⊥BC，

∴∠OBC=90°，

在△OCD和△OCB中，

，

∴△OCD≌△OCB，

∴∠ODC=∠OBC=90°，

∴OD⊥CD，

∴CD是⊙O切线．

（2）如图2中，连接OC交BD于点M，连接OE，

∵AO=OB，AE=EC，

∴OE∥BC，OE=BC，

∴，设EM=a，BM=2a，∠AOE=∠ABC=90°，

∵∠OEM=∠OEB，∠OME=∠EOB=90°，

∴△EOM∽△EBO，

∴EO2=EMEB=a3a

∴EO=a，

同理BO2=BMBE=6a2，

∴BO=AO=a，

∵∠AEO=∠ACB，

∴tan∠ACB=tan∠AEO=．