
����Ŀ�����壺
��ѧ����ϣ�����ʦ�������¶��壺���һ����������һ���ϵ����ߵ��������ߵ�һ�룬��ô��������Ϊ���ǻ���������.

���⣺
����ͼ![]() ����֪
����֪![]() ����
����![]() �����㣬����Բ���ҳ����������ĵ�
�����㣬����Բ���ҳ����������ĵ�![]() ��ʹ
��ʹ![]() Ϊ���ǻ�����������������
Ϊ���ǻ�����������������![]() ��λ�ã�������ͼ�ۼ�����
��λ�ã�������ͼ�ۼ�����
����ͼ![]() ����������
����������![]() ��
��![]() ��
��![]() ���е㣬
���е㣬![]() ��
��![]() ��һ�㣬��
��һ�㣬��![]() �����ж�
�����ж�![]() �Ƿ�Ϊ���ǻ�������������˵�����ɣ�
�Ƿ�Ϊ���ǻ�������������˵�����ɣ�
���ã�
����ͼ![]() ����ƽ��ֱ������ϵ
����ƽ��ֱ������ϵ![]() �У���
�У���![]() �İ뾶Ϊ
�İ뾶Ϊ![]() ����
����![]() ��ֱ��
��ֱ��![]() �ϵ�һ�㣬������
�ϵ�һ�㣬������![]() �ϴ���һ��
�ϴ���һ��![]() ��ʹ��
��ʹ��![]() Ϊ���ǻ������������������ȡ����Сֵʱ��ֱ��д����ʱ��
Ϊ���ǻ������������������ȡ����Сֵʱ��ֱ��д����ʱ��![]() ������.
������.
���𰸡���1�������������2�������������3��P�����꣨��![]() ��
��![]() ������
������![]() ��
��![]() ����
����
�������������������1������AO�����ӳ���Բ��C1������BO�����ӳ���Բ��C2��������⣻��2���������εı߳�Ϊ4a����ʾ��DF=CF�Լ�EC��BE�ij���Ȼ����ݹ��ɶ�����ʽ��ʾ��AF2��EF2��AE2���ٸ��ݹ��ɶ����涨���ж���AEF��ֱ�������Σ���ֱ�������ε����ʿɵ���AEFΪ���ǻ�������������3���������ǻ����������Ķ���ɵ���OPQΪֱ�������Σ���������ɵ�һ��ֱ�DZ�Ϊ1����б�����ʱ����һ��ֱ�DZ���̣������ȡ����Сֵ���ɴ��߶���̿ɵ�б�����Ϊ3�����ݹ��ɶ���������һ��ֱ�DZߣ��ٸ����������������б�ߵĸߣ�����P�ĺ����꣬�ٸ��ݹ��ɶ��������P�������꣬�Ӷ���⣮
���������
��1����ͼ1��ʾ��
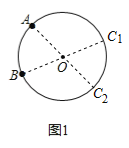
��2����AEF�Ƿ�Ϊ���ǻ������Ρ���
�������£��������εı߳�Ϊ4a��
��E��DC���е㣬
��DE=CE=2a��
��BC��FC=4��1��
��FC=a��BF=4a��a=3a��
��Rt��ADE��AE2=��4a��2+��2a��2=20a2��
��Rt��ECF��EF2=��2a��2+a2=5a2��
��Rt��ABF��AF2=��4a��2+��3a��2=25a2��
��AE2+EF2=AF2��
���AEF��ֱ�������Σ�
��б��AF�ϵ����ߵ���AF��һ�룬
���AEFΪ���ǻ������Ρ���
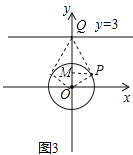
��3����ͼ3��ʾ��
�ɡ��ǻ������Ρ��Ķ���ɵ���OPQΪֱ�������Σ�
��������ɵ�һ��ֱ�DZ�Ϊ1����б�����ʱ����һ��ֱ�DZ���̣������ȡ����Сֵ��
�ɴ��߶���̿ɵ�б�����Ϊ3��
�ɹ��ɶ����ɵ�PQ=![]() ��
��
PM=1��2![]() ��3=
��3=![]() ��
��
�ɹ��ɶ��������OM=![]() ��
��
�ʵ�P�����꣨��![]() ��
��![]() ������
������![]() ��
��![]() ����
����


 ��ҵ����ϵ�д�
��ҵ����ϵ�д� ͬ��ѧ��һ�ζ���ϵ�д�
ͬ��ѧ��һ�ζ���ϵ�д� �����ܾ�ϵ�д�
�����ܾ�ϵ�д� ���ƿ�����ϵ�д�
���ƿ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪��������ʵ��m��n��k����m��n��n��k����m��k��������ȹ�ϵ���д����ԣ�С���ɴ˽������룬������������⣺
��a��b��c��ֱ�ߣ���a��b��b��c����a��c��
��a��b��c��ֱ�ߣ���a��b��b��c����a��c��
����������������࣬������������࣬�������������࣮
������ȷ�������ǣ�������
A.��B.�٢�C.�ڢ�D.�٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѡ���У���������֤�����⡰��a2��1����a��1���Ǽ�����ķ����ǣ� ��
A.a=��2
B.a=��1
C.a=1
D.a=2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC �У���B=32�㣬��C =48�㣬AD��BC�ڵ�D��AEƽ�֡�BAC��BC�ڵ�E��DF��AE�ڵ�F�����ADF�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ����
����![]() Ϊֱ������
Ϊֱ������![]() ���
���![]() �ֱ���
�ֱ���![]() ���㣬����
���㣬����![]() ��
��![]() ��������
��������![]() .
.

����֤��![]() ����
����![]() �����ߣ�
�����ߣ�
����![]() ����
����![]() �ij�
�ij�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���ACB=90�㣬��D��E�ֱ���AC��BC�ϣ�����CDE=��B������CDE��DE�۵�����Cǡ������AB���ϵĵ�F������AC=8��AB=10����CD�ij�Ϊ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���л��Ļ���ԴԶ����������ѧ���棬�����μǡ������������塷����ˮ䰴���������¥�Ρ����ҹ��Ŵ���ƪС˵�еĵ��ʹ���������Ϊ���Ĵ�ŵ���������ij��ѧΪ���˽�ѧ�����Ĵ�ŵ��������Ķ�������͡��Ĵ�ŵ�����������˼���������������ȫУѧ���н����˳������飬���ݵ��������Ƴ���ͼ��ʾ��������������ͳ��ͼ������ͼ����Ϣ����������⣺
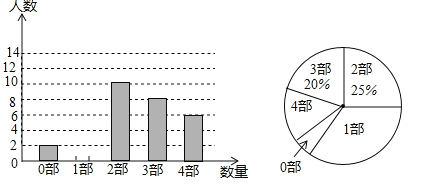
��1�����ε����������ݵ������� ������λ���� ��������ͳ��ͼ�С�1�����������ε�Բ�Ľ�Ϊ �ȣ�
��2���뽫����ͳ��ͼ����������
��3��û�ж����Ĵ�ŵ�����������ѧ�������Ĵ�̶������и������ѡ��һ�����Ķ���������ѡ��ͬһ�����ĸ���Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����������y=3x��ͼ���뷴��������y= ![]() ��ͼ���ڵ�A��1��m���͵�B��
��ͼ���ڵ�A��1��m���͵�B��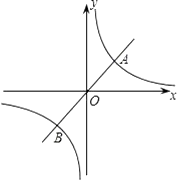
��1����m��ֵ�ͷ����������Ľ���ʽ��
��2���۲�ͼ��ֱ��д��ʹ������������ֵ���ڷ�����������ֵ���Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����м���ԭ��![]() ������ԭ��
������ԭ��![]() ����������ԭ��������
����������ԭ��������![]() ���ֲ�Ʒ��
���ֲ�Ʒ��![]() ������֪����ÿ��
������֪����ÿ��![]() ��Ʒ�����ԭ��
��Ʒ�����ԭ��![]() ������ԭ��
������ԭ��![]() ����ÿ��
����ÿ��![]() ��Ʒ�ɻ��
��Ʒ�ɻ��![]() Ԫ������ÿ��
Ԫ������ÿ��![]() ��Ʒ����ԭ��
��Ʒ����ԭ��![]() ������ԭ��
������ԭ��![]() ����ÿ��
����ÿ��![]() ��Ʒ�ɻ�����
��Ʒ�ɻ�����![]() Ԫ��������
Ԫ��������![]() ��Ʒ
��Ʒ![]() ������Ʒ����Ϊ��������������������Ϣ����������⣺
������Ʒ����Ϊ��������������������Ϣ����������⣺
��1������![]() ���ֲ�Ʒ�ķ������ļ��֣�
���ֲ�Ʒ�ķ������ļ��֣�
��2����������![]() ����Ʒ�ɻ���
����Ʒ�ɻ���![]() Ԫ��д������
Ԫ��д������![]() �ĺ�������ʽ��д����1�����������ķ�����������������.
�ĺ�������ʽ��д����1�����������ķ�����������������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com