
����Ŀ��ij�سǹ���Ҫ�Ӽס��������ֿ���A��B���طֱ�����10�ֺ�5�ֵķ������ʣ��ס������ֿ�ֱ���8�֡�7�ַ������ʣ��Ӽס������ֿ����ͷ������ʵ�A��B���ص��˷ѵ��ۣ�Ԫ/�֣����1����Ӽײֿ����͵�A�صķ�������Ϊx�֣����2����
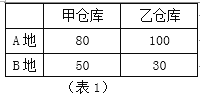

��1����ɱ�2 , ��
��2�������͵����˷�y��Ԫ����x���֣�֮��ĺ�������ʽ����ֱ��д��x��ȡֵ��Χ��
��3��ֱ��д��������˷ѣ�
���𰸡�(1)![]() ��(2)
��(2)![]() ����3��990Ԫ.
����3��990Ԫ.
��������
(1)������������ɣ�
(2)���������ʾ���ײֿ���Ҳֿ�ֱ�����A��B���ۿڵ������������ɵ�����ϵ�����˷ѣ��ײֿ�����A��B�ۿڵķ���+�Ҳֿ�����A��B�ۿڵķ��ã���ʽ�������ɣ�
(3)��Ϊ���õĺ���Ϊһ�κ������ɉ����Կ�֪��y��x��������٣���x=8ʱ��y��С���������Сֵ����
(1)��Ӽײֿ����͵�![]() �صķ�������Ϊ
�صķ�������Ϊ![]() �֣��ɵôӼײֿ����͵�
�֣��ɵôӼײֿ����͵�![]() �صķ�������Ϊ
�صķ�������Ϊ![]() �֣����Ҳֿ����͵�B�صķ�������Ϊ
�֣����Ҳֿ����͵�B�صķ�������Ϊ![]() ��;
��;
�ʴ�Ϊ��![]() ��
��
(2)���͵����˷�y(Ԫ)��x(��)֮��ĺ�������ʽΪ��![]() ������ã�
������ã�![]()
(3)��(2)��![]() ��
��![]() ��
��![]() ��������٣����Ե�
��������٣����Ե�![]() ʱ���˷���С����
ʱ���˷���С����![]() ʱ��
ʱ��![]() ��������˷�Ϊ990Ԫ.
��������˷�Ϊ990Ԫ.


 ѧҵ����һ��һ��ϵ�д�
ѧҵ����һ��һ��ϵ�д� Сѧ��ʱ��ҵȫͨ����ϵ�д�
Сѧ��ʱ��ҵȫͨ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������ABC�ĵױ�BC��Ϊ4�������16����AC�Ĵ�ֱƽ����EF�ֱ�AC��AB����E��F��![]() ����DΪBC�ߵ��е㣬��MΪ�߶�EF��һ���㣬��
����DΪBC�ߵ��е㣬��MΪ�߶�EF��һ���㣬��![]() �ܳ�����СֵΪ
�ܳ�����СֵΪ![]() ����
����![]()

A. 6 B. 8 C. 10 D. 12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=2��AD=4��AC�Ĵ�ֱƽ����EF��AD�ڵ�E����BC�ڵ�F����EF�ij�Ϊ��������
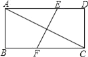
A. 4 B. 2![]() C.
C. ![]() D. 2
D. 2![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣���֪����ֱ��![]() �У�BDΪб���ϵ����ߣ�EΪDC�ϵ�һ�㣬��
�У�BDΪб���ϵ����ߣ�EΪDC�ϵ�һ�㣬��![]() ��G��AG��BD��F.
��G��AG��BD��F.
��1����֤��AF=BE.
��2����ͼ�ڣ�����E��DC���ӳ����ϣ������������䣬�ٵĽ��ۻ��ܳ����������ܣ���˵�����ɣ����ܣ�������֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʦΪ���˽�ѧ�������ڼҵ��Ķ���������������20��ѧ��ijһ����Ķ�Сʱ�����������ͳ�����£�
�Ķ�ʱ�� ��Сʱ�� | 2 | 2.5 | 3 | 3.5 | 4 |
ѧ������������ | 1 | 2 | 8 | 6 | 3 |
�������20��ѧ���Ķ�Сʱ����˵����ȷ���ǣ�������
A. ������8 B. ��λ����3 C. ƽ������3 D. ������0.34
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������1+3+32+34+35+36+37+38��ֵʱ���ź췢�֣��ӵڶ���������ÿһ����������ǰһ��������3�������������裺S=1+3+32+33+34+35+36+37+38�٣�Ȼ���ڢ�ʽ�����߶�����3���ã�3S=3+32+33+34+35+36+37+38+39���������ٵã�3S��S=39��1����2S=39��1����S=![]() ��
��
���Ķ��ź췢�ֵĹ��ɣ������ź����������⣺
��1�������Խ���ź��룺�������3��������ĸm��m��0��m��1����Ӧ��������ȵķ������1+m+m2+m3+m4+��+m2018��ֵ���Ը�ʽ��ֵ����IJ�����______���ú�m�Ĵ���ʽ��ʾ����
��2��֤����IJ�������ȷ�ģ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ʾ��ֱ��L��y=mx+5m��x�Ḻ���ᣬy��������ֱ���A��B���㣮
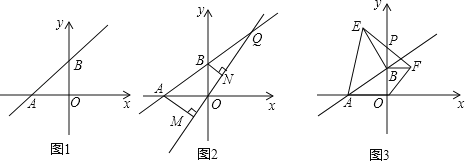
��1����OA=OBʱ�����A���꼰ֱ��L�Ľ���ʽ��
��2���ڣ�1���������£���ͼ����ʾ����QΪAB�ӳ�����һ�㣬��ֱ��OQ����A��B����ֱ���AM��OQ��M��BN��OQ��N����AM=4����BN�ij���
��3����mȡ��ͬ��ֵʱ����B��y�����������˶����ֱ���OB��ABΪ�ߣ���BΪֱ�Ƕ����ڵ�һ����������������ֱ����OBF�͵���ֱ����ABE����EF��y����P�㣬��ͼ�ۣ�
�ʣ�����B��y�����������˶�ʱ���Բ���PB�ij��Ƿ�Ϊ��ֵ�����ǣ��������ֵ�������ǣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ��Ϊֱ���ġ�
��Ϊֱ���ġ�![]() ������
������![]() ,
,![]() �ǡ�
�ǡ�![]() ��һ�㣬����
��һ�㣬����![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() .
.
��1�����ж�![]() ���
���![]() ��λ�ù�ϵ����˵�����ɣ�
��λ�ù�ϵ����˵�����ɣ�
��2������![]() �ǻ�
�ǻ�![]() ���е㣬��֪
���е㣬��֪![]() ����
����![]() ��ֵ.
��ֵ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�AC��BD���ڵ�M����F��AD�ϣ�AF=6cm��BF=12cm����FBM=��CBM����E��BC���е㣬����P��1cm/s����ٶȴӵ�A��������AD���F�˶�����Qͬʱ��2cm/����ٶȴӵ�C��������CB���B�˶�����P�˶���F��ʱֹͣ�˶�����QҲͬʱֹͣ�˶�������P�˶�__��ʱ����P��Q��E��FΪ������ı�����ƽ���ı��Σ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com