
【题目】两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,在探究筝形的性质时,得到如下结论:①△ABD≌△CBD;②AC⊥BD;③四边形ABCD的面积= ![]() ACBD,其中正确的结论有( )
ACBD,其中正确的结论有( ) 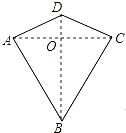
A.0个
B.1个
C.2个
D.3个
科目:初中数学 来源: 题型:
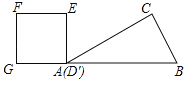
【题目】如图,Rt△ABC中∠C=90°,∠BAC=30°,AB=8,以![]() 为边长的正方形DEFG的一边CD在直线AB上,且点D与点A重合,现将正方形DEFG沿A﹣B的方向以每秒1个单位的速度匀速运动,当点D与点B重合时停止,则在这个运动过程中,正方形DEFG与△ABC的重合部分的面积S与运动时间t之间的函数关系图象大致是( )
为边长的正方形DEFG的一边CD在直线AB上,且点D与点A重合,现将正方形DEFG沿A﹣B的方向以每秒1个单位的速度匀速运动,当点D与点B重合时停止,则在这个运动过程中,正方形DEFG与△ABC的重合部分的面积S与运动时间t之间的函数关系图象大致是( )
A. B.
B.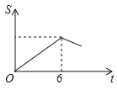 C.
C.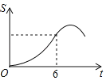 D.
D.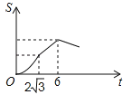
查看答案和解析>>
科目:初中数学 来源: 题型:
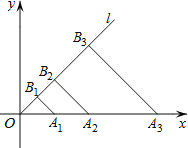
【题目】如图,在平面直角坐标系xOy中,点A1,A2,A3,…,An在x轴的正半轴上,且OA1=2,OA2=2OA1,OA3=2OA2,…,OAn=2OAn﹣1,点B1,B2,B3,…,Bn在第一象限的角平分线l上,且A1B1,A2B2,…,AnBn都与射线l垂直,则B1的坐标是 ,B3的坐标是 ,Bn的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一项工程,若由甲、乙两公司合作18天可以完成,共需付施工费144000元,若甲、乙两公司单独完成此项工程,甲公司所用时间是乙公司的1.5倍,已知甲公司每天的施工费比乙公司每天的施工费少2000元.
(1)求甲、乙两公司单独完成此项工程,各需多少天?
(2)若由一个公司单独完成这项工程,哪个公司的施工费较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2﹣(2k﹣1)x+k2﹣1=0,其中k<0.
(1)求证:方程有两个不相等的实数根;
(2)当k=﹣1时,求该方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
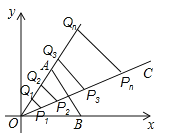
【题目】如图,在直角坐标系xOy中,点A在第一象限,点B在x轴的正半轴上,△AOB为正三角形,射线OC⊥AB,在OC上依次截取点P1,P2,P3,…,Pn,使OP1=1,P1P2=3,P2P3=5,…,Pn﹣1Pn=2n﹣1(n为正整数),分别过点P1,P2,P3,…,Pn向射线OA作垂线段,垂足分别为点Q1,Q2,Q3,…,Qn,则点Qn的坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com