
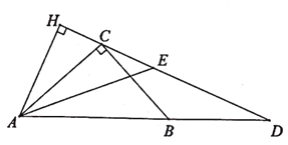
【题目】如衅,在Rt△ABC中,∠ACB=90°,sin∠BAC=![]() ,点D在AB的延长线上,BD=BC,AE平分∠BAC交CD于点E,若AE=5
,点D在AB的延长线上,BD=BC,AE平分∠BAC交CD于点E,若AE=5![]() ,则点A到直线CD的距离AH为________,BD的长为________.
,则点A到直线CD的距离AH为________,BD的长为________.
【答案】5; 2![]()
【解析】
证明HA=HE,理由等腰直角三角形的性质即可求出AH,由sin∠BAC=![]() ,设BC=BD=2k,AB=3k,则AC=
,设BC=BD=2k,AB=3k,则AC=![]() k,证明△HAC∽△HDA,可得AH2=HCHD,由△AHC∽△CMB,可得
k,证明△HAC∽△HDA,可得AH2=HCHD,由△AHC∽△CMB,可得![]() ,推出
,推出![]() ,推出CM=2
,推出CM=2![]() ,CD=4
,CD=4![]() ,可得25=HC(HC+4
,可得25=HC(HC+4![]() ),求出CH即可解决问题.
),求出CH即可解决问题.
如图,作BM⊥CD于M.

∵BC=BD,
∴∠D=∠BCD,
∵AH⊥DH,
∴∠H=∠ACB=90°,
∴∠ACH+∠HAC=90°,∠ACH+∠BCD=90°,
∴∠HAC=∠BCD=∠D,
∵AE平分∠CAB,
∴∠EAC=∠EAD,
∵∠HAE=∠HAC+∠EAC,∠AEH=∠D+∠EAD,
∴∠HAE=∠AEH,
∴HA=HE,
∵AE=5![]() ,
,
∴AH=HE=5,
∵sin∠BAC=![]() ,设BC=BD=2k,AB=3k,则AC=
,设BC=BD=2k,AB=3k,则AC=![]() k,
k,
∵∠H=∠H,∠HAC=∠D,
∴△HAC∽△HDA,
∴AH2=HCHD,
∵∠BCM=∠HAC,∠H=∠BMC=90°,
∴△AHC∽△CMB,
∴![]() ,
,
∴![]() ,
,
∴CM=2![]() ,
,
∵BC=BD,BM⊥CD,
∴CM=DM=2![]() ,
,
∴CD=4![]() ,
,
∴25=HC(HC+4![]() ),
),
∴HC=![]() 或-5
或-5![]() (舍弃),
(舍弃),
∴AC=![]() ,
,
∴![]() k=
k=![]() ,
,
∴k=![]() ,
,
∴BD=CB=2k=2![]() ,
,
故答案为5,2![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】“数学来源于生活,又运用于生活”曹老师为了了解所教班级学生利用数学知识解决实际问题的能力,编制若干问题对全班学生进行了一次测试,并将测试结果分成四类,A特别强:B:强;C:一般:D较弱以下是由调查测试结果绘制的两幅不完整的统计图,请你根据统计图完成以下解答.
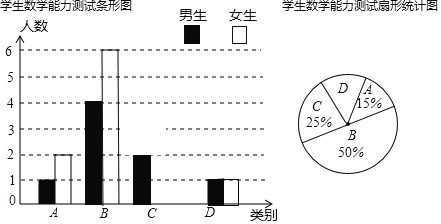
(1)曹老师的班级共有 名学生;
(2)将下面条形统计图的C类部分补充完整;
(3)扇形统计图中,D类对应的圆心角为多少度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知抛物线y=ax2+bx+c的图像经过点A(0,3)、B(1,0),其对称轴为直线l:x=2,过点A作AC∥x轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点,设其横坐标为m.

(1)求抛物线的解析式;
(2)若动点P在直线OE下方的抛物线上,连结PE、PO,当m为何值时,四边形AOPE面积最大,并求出其最大值;
(3)如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
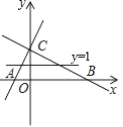
【题目】如图,直线y1=2x+2交x轴、y轴于点A、C,直线![]() 交x轴、y轴于点B、C,点P(m,1)是△ABC内部(包括边上)的一点,则m的最大值与最小值之差为( )
交x轴、y轴于点B、C,点P(m,1)是△ABC内部(包括边上)的一点,则m的最大值与最小值之差为( )
A.2B.2.5C.3D.3.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【探索新知】:如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.
(1)一个角的平分线 这个角的“巧分线”;(填“是”或“不是”)
(2)如图2,若∠MPN=α,且射线PQ是∠MPN的“巧分线”,则∠MPQ= ;(用含α的代数式表示出所有可能的结果)
【深入研究】:如图2,若∠MPN=60°,且射线PQ绕点P从PN位置开始,以每秒10°的速度逆时针旋转,当PQ与PN成180°时停止旋转,旋转的时间为t秒.
(3)当t为何值时,射线PM是∠QPN的“巧分线”;
(4)若射线PM同时绕点P以每秒5°的速度逆时针旋转,并与PQ同时停止,请直接写出当射线PQ是∠MPN的“巧分线”时t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一块矩形地皮,计划共分九个区域区域甲、乙是两个矩形主体建筑,区域丙为梯形停车场,区城①-④是四块三角形绿化区,△AEL和△CIJ为综合办公区(如图所示).∠HEL=∠ELI=90°,MN//BC.AD=220米,AL=40米,AE=IC=30米.
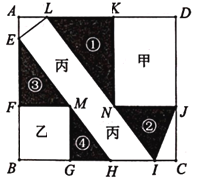
(1)求HI的长
(2)若BG=KD,求主体建筑甲和乙的面积和.
(3)设LK=3x米,绿化区②的面积为S平方米.若要求绿化区②与④的面积之差不少于1200平方米,求S关于x的函数表达式.并求出S的最小值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)如果⊙O的半径为![]() ,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.

【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)首先连接OD,由OE∥AB,根据平行线与等腰三角形的性质,易证得![]() ≌
≌![]() 即可得
即可得![]() ,则可证得
,则可证得![]() 为
为![]() 的切线;
的切线;
(2)连接CD,根据直径所对的圆周角是直角,即可得![]() 利用勾股定理即可求得
利用勾股定理即可求得![]() 的长,又由OE∥AB,证得
的长,又由OE∥AB,证得![]() 根据相似三角形的对应边成比例,即可求得
根据相似三角形的对应边成比例,即可求得![]() 的长,然后利用三角函数的知识,求得
的长,然后利用三角函数的知识,求得![]() 与
与![]() 的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
试题解析:(1)证明:连接OD,

∵OE∥AB,
∴∠COE=∠CAD,∠EOD=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠COE=∠DOE,
在△COE和△DOE中,
 ∴△COE≌△DOE(SAS),
∴△COE≌△DOE(SAS),
![]()
∴ED⊥OD,
∴ED是![]() 的切线;
的切线;
(2)连接CD,交OE于M,
在Rt△ODE中,
∵OD=32,DE=2,
![]()
∵OE∥AB,
∴△COE∽△CAB,
![]() ∴AB=5,
∴AB=5,
∵AC是直径,
![]()
![]()
![]()
![]()
∵EF∥AB,
![]()
![]()
![]()
∴S△ADF=S梯形ABEFS梯形DBEF
![]()
∴△ADF的面积为![]()

【题型】解答题
【结束】
25
【题目】【题目】已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b.
(1)求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);
(2)直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;
(3)a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
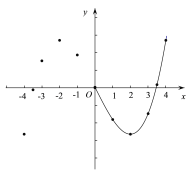
【题目】有这样一个问题:探究函数![]() 的图象与性质.小彤根据学习函数的经验,对函数
的图象与性质.小彤根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小彤探究的过程,请补充完整:
的图象与性质进行了探究.下面是小彤探究的过程,请补充完整:
x | -4 | -3.5 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 3.5 | 4 | ||
y |
|
|
|
|
| 0 |
|
| m |
|
|
(1)求m的值为 ;
(2)如图,在平面直角坐标系x0y 中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出了图象的一部分,请根据剩余的点补全此函数的图象;
(3)方程![]() 实数根的个数为 ;
实数根的个数为 ;
(4)观察图象,写出该函数的一条性质 ;
(5)在第(2)问的平面直角坐标系中画出直线![]() ,根据图象写出方程
,根据图象写出方程![]() 的一个正数根约为 (精确到0.1).
的一个正数根约为 (精确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
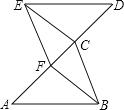
【题目】如图,已知A、F、C、D四点在同一条直线上,AF=CD,AB∥DE,且AB=DE.
(1)求证:△ABC≌△DEF;
(2)若EF=3,DE=4,∠DEF=90°,请直接写出使四边形EFBC为菱形时AF的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com