
【题目】现有一块矩形地皮,计划共分九个区域区域甲、乙是两个矩形主体建筑,区域丙为梯形停车场,区城①-④是四块三角形绿化区,△AEL和△CIJ为综合办公区(如图所示).∠HEL=∠ELI=90°,MN//BC.AD=220米,AL=40米,AE=IC=30米.
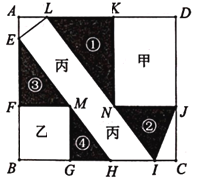
(1)求HI的长
(2)若BG=KD,求主体建筑甲和乙的面积和.
(3)设LK=3x米,绿化区②的面积为S平方米.若要求绿化区②与④的面积之差不少于1200平方米,求S关于x的函数表达式.并求出S的最小值
【答案】(1)![]() ;(2)15750;(3)当x=30时,S最小值=3600.
;(2)15750;(3)当x=30时,S最小值=3600.
【解析】
(1)过H作HP⊥LI于点P,得四边形EHPL为矩形,得HP=EL=50米,再证∠PHI=∠ALE,由cos∠ALE便可求得HI;
(2)设BG=KD=x米,用x表示KL、GH,进而通过三角函数用x表示KN、MG、EF,再由AE+EF=KN,列出x的方程,求出x的值便可;
(3)由三角函数用x表示KN,进而表示FM、GH、MG,再已知条件“绿化区②与④的面积之差不少于1200平方米”列出不等式,求出x的取值范围,进而由三角形面积公式表示出S与x的函数关系式,最后由函数性质求出最小值.
(1)过H作HP⊥LI于点P,如图所示,
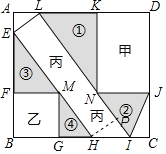
则四边形EHPL为矩形,HP=EL=![]() ,
,
∵∠A=∠B=∠EHP=90°,
∴∠PHI+∠BHE=∠BHE+∠BEH=∠BEH+∠AEL=∠AEL+∠ALE=90°,
∴∠ALE=∠PHI,
∴![]() ,
,
∴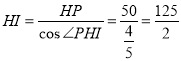 ,
,
答:HI的长度为![]() 米;
米;
(2)设BG=KD=x米,则GH=220-x-![]() -30=
-30=![]() -x,LK=220-40-x=180-x,FM=x,
-x,LK=220-40-x=180-x,FM=x,
由互余角性质,易证∠KLN=∠AEL=∠EMF=∠MHG,
∴tan∠KLN=tan∠EMF=tan∠MHG=tan∠AEL=![]() ,
,
∴KN=LKtan∠KLN=240-![]() x,
x,
EF=MFtan∠EMF=![]() x,
x,
MG=GHtan∠MHG=170-![]() x,
x,
∵MN∥BC∥AD,
∴AF=KN,即30+![]() x=240-
x=240-![]() x,
x,
解得,x=![]() ,
,
∴主体建筑甲和乙的面积和为:BGGM+DKKN=![]() ×(170-
×(170-![]() ×
×![]() )+
)+![]() ×(240-
×(240-![]() ×
×![]() )=15750,
)=15750,
答:主体建筑甲和乙的面积和15750平方米;
(3)∵LK=3x,
∴KN=LKtan∠KLN=3x×![]() =4x,NJ=KD=220-40-3x=180-3x,
=4x,NJ=KD=220-40-3x=180-3x,
∴BG=FM=220-NJ-MN=220-180+3x-![]() =3x-
=3x-![]() ,
,
∴GH=220-BG-HI-IC=220-3x+![]() -
-![]() -30=150-3x,
-30=150-3x,
∴GM=GHtan∠GHM=200-4x,
∵绿化区②与④的面积之差不少于1200平方米,
∴![]() NJGM-
NJGM-![]() GHGM≥1200,
GHGM≥1200,
即![]() (180-3x)(200-4x)-
(180-3x)(200-4x)-![]() (150-3x)(200-4x)≥1200,
(150-3x)(200-4x)≥1200,
解得,x≤30,
∵S=![]() NJGM=
NJGM=![]() (180-3x)(200-4x)=6(x-55)2-25,
(180-3x)(200-4x)=6(x-55)2-25,
∴当x<55时,S随x的增大而减小,
∴当x=30时,S有最小值为:S=6(30-55)2-25=3600.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】如图,D,E分别是△ABC的边AB,AC的中点,H,G是边BC上的点,且HG=![]() BC,S△ABC=24,则图中阴影部分的面积为( )
BC,S△ABC=24,则图中阴影部分的面积为( )

A. 4B. 6C. 8D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
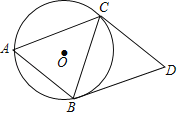
【题目】如图,已知⊙O是△ABC的外接圆,且AB=BC=CD,AB∥CD,连接BD.
(1)求证:BD是⊙O的切线;
(2)若AB=10,cos∠BAC=![]() ,求BD的长及⊙O的半径.
,求BD的长及⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我渔政310船在南海海面上沿正东方向匀速航行,在A地观测到我渔船C在东北方向上的我国某传统渔场.若渔政310船航向不变,航行半小时后到达B处,此时观测到我渔船C在北偏东30°方向上.问渔政310船再航行多久,离我渔船C的距离最近?(假设我渔船C捕鱼时移动距离忽略不计,结果不取近似值.)
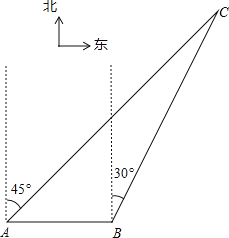
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如衅,在Rt△ABC中,∠ACB=90°,sin∠BAC=![]() ,点D在AB的延长线上,BD=BC,AE平分∠BAC交CD于点E,若AE=5
,点D在AB的延长线上,BD=BC,AE平分∠BAC交CD于点E,若AE=5![]() ,则点A到直线CD的距离AH为________,BD的长为________.
,则点A到直线CD的距离AH为________,BD的长为________.
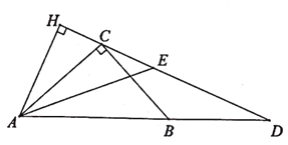
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2015南通)如图,在ABCD中,点E,F分别在AB,DC上,且ED⊥DB,FB⊥BD.
(1)求证:△AED≌△CFB;
(2)若∠A=30°,∠DEB=45°,求证:DA=DF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学家赵爽利用弦图证明了勾股定理,这是著名的赵爽弦图(如图1).它是由四个全等的直角三角形拼成了内、外都是正方形的美丽图案.在弦图中(如图2),已知点O为正方形ABCD的对角线BD的中点,对角线BD分别交AH,CF于点P、Q.在正方形EFGH的EH、FG两边上分别取点M,N,且MN经过点O,若MH=3ME,BD=2MN=4![]() .则△APD的面积为_____.
.则△APD的面积为_____.
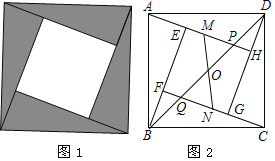
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌牛奶供应商提供A,B,C,D四种不同口味的牛奶供学生饮用.某校为了了解学生对不同口味的牛奶的喜好,对全校订牛奶的学生进行了随机调查,并根据调查结果绘制了如下两幅不完整的统计图.根据统计图的信息解决下列问题:
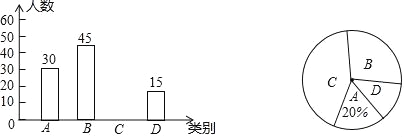
(1)本次调查的学生有多少人?
(2)补全上面的条形统计图;
(3)扇形统计图中C对应的中心角度数是_____;
(4)若该校有600名学生订了该品牌的牛奶,每名学生每天只订一盒牛奶,要使学生能喝到自己喜欢的牛奶,则该牛奶供应商送往该校的牛奶中,A,B口味的牛奶共约多少盒?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com