
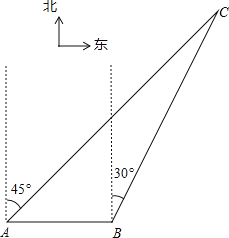
【题目】如图,我渔政310船在南海海面上沿正东方向匀速航行,在A地观测到我渔船C在东北方向上的我国某传统渔场.若渔政310船航向不变,航行半小时后到达B处,此时观测到我渔船C在北偏东30°方向上.问渔政310船再航行多久,离我渔船C的距离最近?(假设我渔船C捕鱼时移动距离忽略不计,结果不取近似值.)
【答案】渔政310船再航行15(![]() +1)分钟,离我渔船C的距离最近.
+1)分钟,离我渔船C的距离最近.
【解析】过点C作AB的垂线,设垂足为D.由题易知∠CAB=45°,∠CBD=60°.先在Rt△BCD中,得到CD=![]() BD,再在Rt△ACD中,得到CD=AD,据此得出
BD,再在Rt△ACD中,得到CD=AD,据此得出![]() ,然后根据匀速航行的渔船其时间之比等于路程之比,从而求出渔船行驶BD的路程所需的时间.
,然后根据匀速航行的渔船其时间之比等于路程之比,从而求出渔船行驶BD的路程所需的时间.
作CD⊥AB交AB的延长线于点D.
∵A地观测到渔船C在东北方向上,渔船C在北偏东30°方向上,
∴∠CAB=45°,∠CBD=60°.
在Rt△BCD中,∵∠CDB=90°,∠CBD=60°,
∴CD=![]() BD.
BD.
在Rt△ACD中,∵∠CDA=90°,∠CAD=45°,
∴CD=AD,
∴![]() BD=AB+BD,
BD=AB+BD,
∴![]() ,
,
设渔政310船再航行t分钟,离我渔船C的距离最近,
则![]() ,
,
解得t=15![]() +15.
+15.
答:渔政310船再航行(15![]() +15)分钟,离我渔船C的距离最近.
+15)分钟,离我渔船C的距离最近.


科目:初中数学 来源: 题型:
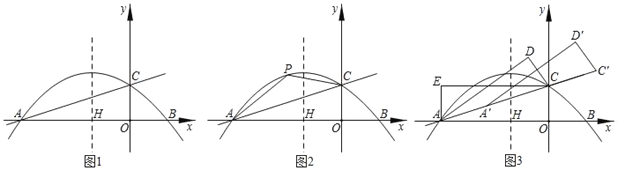
【题目】已知抛物线y=﹣![]() x2﹣
x2﹣![]() x+2与x轴交于点A,B两点,交y轴于C点,抛物线的对称轴与x轴交于H点,分别以OC、OA为边作矩形AECO.
x+2与x轴交于点A,B两点,交y轴于C点,抛物线的对称轴与x轴交于H点,分别以OC、OA为边作矩形AECO.
(1)求直线AC的解析式;
(2)如图2,P为直线AC上方抛物线上的任意一点,在对称轴上有一动点M,当四边形AOCP面积最大时,求|PM﹣OM|的最大值.
(3)如图3,将△AOC沿直线AC翻折得△ACD,再将△ACD沿着直线AC平移得△A'C′D'.使得点A′、C'在直线AC上,是否存在这样的点D′,使得△A′ED′为直角三角形?若存在,请求出点D′的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
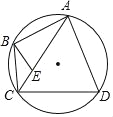
【题目】如图,四边形ABCD为圆内接四边形,A为弧BD中点,连接对角线AC,E在AC上,且AE=AB求证:
(1)∠CBE=![]() ∠CAD;
∠CAD;
(2)AC2=BCCD+AB2.
查看答案和解析>>
科目:初中数学 来源: 题型:
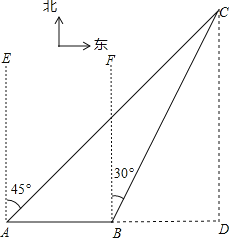
【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OABC中顶点A在x轴负半轴上,B、C在第二象限,对角线交于点D,若C、D两点在反比例函数![]() 的图象上,且OABC的面积等于12,则k的值是____.
的图象上,且OABC的面积等于12,则k的值是____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某小组同学为了测量对面楼AB的高度,分工合作,有的组员测得两楼间距离为40米,有的组员在教室窗户处测得楼顶端A的仰角为30°,底端B的俯角为10°,请你根据以上数据,求出楼AB的高度.(精确到0.1米)
(参考数据:sin10°≈0.17, cos10°≈0.98, tan10°≈0.18, ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽和小华想利用摸球游戏决定谁去参加市里举办的书法比赛,游戏规则是:在一个不透明的袋子里装有除数字外完全相同的4个小球,上面分别标有数字2,3,4,5.一人先从袋中随机摸出一个小球,另一人再从袋中剩下的3个小球中随机摸出一个小球.若摸出的两个小球上的数字和为偶数,则小丽去参赛;否则小华去参赛.
(1)用列表法或画树状图法,求小丽参赛的概率.
(2)你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com