
【题目】如图,AB是⊙O的直径,弦BC垂直且平分半径OD,AB=6,
(1)求∠ABC的度数;
(2)求BC的长.
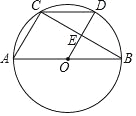
【答案】(1)∠ABC=30°;(2)BC=3![]() .
.
【解析】
(1)通过连接BD,因为弦BC垂直且平分半径OD,可得BO=BD,又因为BO=OD(都是半径),可知BO=BD=OD,则△ODB是等边三角形,得到∠ABD=60°,再利用等腰三角形三线合一,即可求出∠ABC度数.
(2)AB是直径,可知△ACB是直角三角形,解这个直角三角形即可得到答案.
解:(1)如图连接BD.

∵BC垂直平分线段OD,
∴BO=BD,
∵OD=OB,
∴OD=OB=BD,
∴△ODB是等边三角形,
∴∠ABD=60°,
∵BE⊥OD,
∴∠ABC=![]() ∠OBD=30°,
∠OBD=30°,
(2)
∵AB是直径,
∴∠ACB=90°,
∵AB=6,∠ABC=30°,
∴BC=ABcos30°=3![]() .
.


科目:初中数学 来源: 题型:
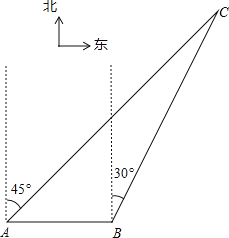
【题目】如图,我渔政310船在南海海面上沿正东方向匀速航行,在A地观测到我渔船C在东北方向上的我国某传统渔场.若渔政310船航向不变,航行半小时后到达B处,此时观测到我渔船C在北偏东30°方向上.问渔政310船再航行多久,离我渔船C的距离最近?(假设我渔船C捕鱼时移动距离忽略不计,结果不取近似值.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】热气球的探测器显示,从热气球底部A处看一栋高楼顶部的俯角为30°,看这栋楼底部的俯角为60°,热气球A处与地面距离为420米,求这栋楼的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
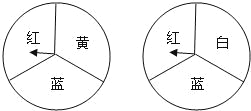
【题目】小明和小刚用如图所示的两个转盘做配紫色游戏,游戏规则是:分别旋转两个转盘,若其中一个转盘转出了红色,另一个转出了蓝色则可以配成紫色.此时小刚得1分,否则小明得1分.这个游戏规则对双方公平吗?请说明理由.若你认为不公平,如何修改规则才能使游戏对双方公平?
查看答案和解析>>
科目:初中数学 来源: 题型:
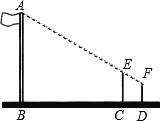
【题目】在一次数学活动课上,老师让同学们到操场上测量旗杆的高度,然后回来交流各自的测量方法.小芳的测量方法是:拿一根高3.5米的竹竿直立在离旗杆27米的C处(如图),然后沿BC方向走到D处,这时目测旗杆顶部A与竹竿顶部E恰好在同一直线上,又测得C、D两点的距离为3米,小芳的目高为1.5米,这样便可知道旗杆的高.你认为这种测量方法是否可行?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB经过圆心O,交⊙O于点A、C,点D为⊙O上一点,连结AD、OD、BD,∠BAD=∠B=30°.
(1)求证:BD是⊙O的切线.
(2)若OA=8,求OA、OD与![]() 围成的扇形的面积.
围成的扇形的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
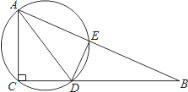
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=5,CB=12,AD是△ABC的角平分线,过A、C、D三点的圆与斜边AB交于点E,连接DE.
(1)求BE的长;(2)求△ACD外接圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△AOB中,C,D分别是OA、OB边上的点,将△OCD绕点O顺时针旋转到△OC′D′.如图,若∠AOB=90°,OA=OB,C,D分别为OA,OB的中点.求证:
(1)AC′=BD′;
(2)AC′⊥BD.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com