
【题目】如图,四边形ABCD为圆内接四边形,A为弧BD中点,连接对角线AC,E在AC上,且AE=AB求证:
(1)∠CBE=![]() ∠CAD;
∠CAD;
(2)AC2=BCCD+AB2.
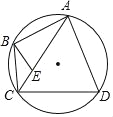
【答案】(1)证明见解析 (2)证明见解析
【解析】
(1)连接BD交AC于F,根据圆的性质得:∠ABD=∠ACB=∠ACD,由等腰三角形的性质得:∠ABE=∠AEB,根据外角的性质得:∠CBE=∠DBE,从而得结论;
(2)先根据两角相等两三角形相似证明:△ACD∽△BCF和△ABF∽△ACB,列比例式后,化为乘积式后相加可得结论.
证明:(1)连接BD交AC于F,
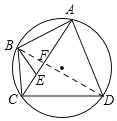
∵A为弧BD中点,
∴弧AB=弧AD,
∴∠ABD=∠ACB=∠ACD,
∵AB=AE,
∴∠ABE=∠AEB,
∵∠AEB=∠ACB+∠CBE,∠ABE=∠ABD+∠DBE,
∴∠CBE=∠DBE,
∵∠CAD=∠CBD=2∠CBE,
∴∠CBE=![]() ∠CAD,
∠CAD,
(2)∵∠DBC=∠CAD,∠ACB=∠ACD,
∴△ACD∽△BCF,
∴![]() ,
,
∴BCCD=ACCF①,
∵∠ABF=∠ACB,∠BAF=∠CAB,
∴△ABF∽△ACB,
∴![]() ,
,
∴AB2=ACAF②,
①+②得:AB2+BCCD=ACCF+ACAF=AC(CF+AF),
∴AC2=BCCD+AB2.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
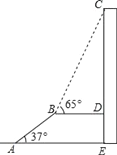
【题目】如图,AB是长为10m,倾斜角为37°的自动扶梯,平台BD与大楼CE垂直,且与扶梯AB的长度相等,在B处测得大楼顶部C的仰角为65°,求大楼CE的高度(结果保留整数).
(参考数据:sin37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin65°≈
,sin65°≈![]() ,tan65°≈
,tan65°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
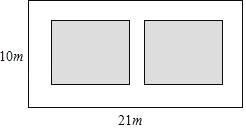
【题目】如图,有一块长为21m、宽为10m的矩形空地,计划在其中修建两块相同的矩形绿地,两块绿地之间及周边留有宽度相等的人行通道,且人行通道的宽度不能超过3米.
(1)如果两块绿地的面积之和为90m2,求人行通道的宽度;
(2)能否改变人行通道的宽度,使得每块绿地的宽与长之比等于3:5,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
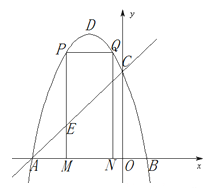
【题目】如图,抛物线![]() 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N.若点P在点Q左边,当矩形PQMN的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ.过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG=![]() DQ,求点F的坐标.
DQ,求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正△ABC的顶点B(﹣3,0)、C(﹣1,0),过坐标原点O的一条直线分别与边AB、AC交于点M、N.若OM=2ON,则点N的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
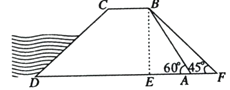
【题目】如图,水坝的横断面是梯形,背水坡AB的坡角∠BAD=![]() ,坡长AB=
,坡长AB=![]() ,为加强水坝强度,将坝底从A处向后水平延伸到F处,使新的背水坡的坡角∠F=45
,为加强水坝强度,将坝底从A处向后水平延伸到F处,使新的背水坡的坡角∠F=45![]() ,求AF的长度(结果精确到1米,参考数据:
,求AF的长度(结果精确到1米,参考数据: ![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
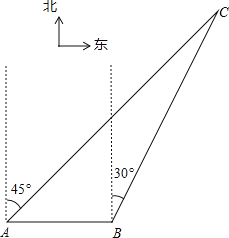
【题目】如图,我渔政310船在南海海面上沿正东方向匀速航行,在A地观测到我渔船C在东北方向上的我国某传统渔场.若渔政310船航向不变,航行半小时后到达B处,此时观测到我渔船C在北偏东30°方向上.问渔政310船再航行多久,离我渔船C的距离最近?(假设我渔船C捕鱼时移动距离忽略不计,结果不取近似值.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠A=110°,点E是菱形ABCD内一点,连结CE绕点C顺时针旋转110°,得到线段CF,连结BE,DF,若∠E=86°,求∠F的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
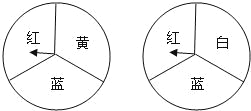
【题目】小明和小刚用如图所示的两个转盘做配紫色游戏,游戏规则是:分别旋转两个转盘,若其中一个转盘转出了红色,另一个转出了蓝色则可以配成紫色.此时小刚得1分,否则小明得1分.这个游戏规则对双方公平吗?请说明理由.若你认为不公平,如何修改规则才能使游戏对双方公平?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com