
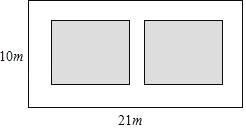
【题目】如图,有一块长为21m、宽为10m的矩形空地,计划在其中修建两块相同的矩形绿地,两块绿地之间及周边留有宽度相等的人行通道,且人行通道的宽度不能超过3米.
(1)如果两块绿地的面积之和为90m2,求人行通道的宽度;
(2)能否改变人行通道的宽度,使得每块绿地的宽与长之比等于3:5,请说明理由.
【答案】(1)2米;(2)不能改变人行横道的宽度使得每块绿地的宽与长之比等于3:5.
【解析】
(1)设人行通道的宽度为x米,将两块矩形绿地的长和宽用含有x的式子表示出来,根据“两块矩形绿地的面积共为90平方米”列出关于x的一元二次方程,解之即可;(2)根据每块绿地的宽与长之比等于3:5列出方程求得人行横道的宽度后与3米比较即可得到答案.
(1)设人行通道的宽度为x米,
则两块矩形绿地的长为(21﹣3x)(米),
宽为(10﹣2x)(米),
根据题意得:(21﹣3x)(10﹣2x)=90,
解得:x1=10(舍去),x2=2,
答:人行通道的宽度为2米;
(2)设人行通道的宽为y米时,每块绿地的宽与长之比等于3:5,
根据题意得:(10﹣2y):![]() =3:5,
=3:5,
解得:y=![]() ,
,
∵![]() >3,
>3,
∴不能改变人行横道的宽度使得每块绿地的宽与长之比等于3:5.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
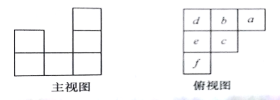
【题目】用小立方体搭一个几何体,使它的主视图和俯视图如图所示,俯视图中小正方形中字母表示在该位置小立方体的个数,请解答下列问题:
(1)求![]() 的值;
的值;
(2)这个几何体最少有几个小立方体搭成,最多有几个小立方体搭成;
(3)当![]() 时画出这个几何体的左视图.
时画出这个几何体的左视图.
查看答案和解析>>
科目:初中数学 来源: 题型:
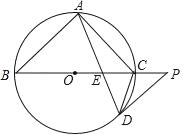
【题目】如图,已知BC是⊙O的直径,点A,D在⊙O上,∠B=2∠CAD,在BC的延长线上有一点P,使得∠P=∠ACB,弦AD交直径BC于点E.
(1)求证:DP与⊙O相切;
(2)判断△DCE的形状,并证明你的结论;
(3)若CE=2,DE=![]() ,求线段BC的长度.
,求线段BC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
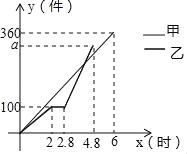
【题目】甲、乙两组工人同时开始加工某种零件,乙组在工作中有一次停产更换设备,更换设备后,乙组的工作效率是原来的2倍.两组各自加工零件的数量y(件)与时间x(时)之间的函数图象如图所示.甲、乙两组加工出的零件合在一起装箱,每够300件装一箱,零件装箱的时间忽略不计,求经过_____小时恰好装满第1箱.
查看答案和解析>>
科目:初中数学 来源: 题型:
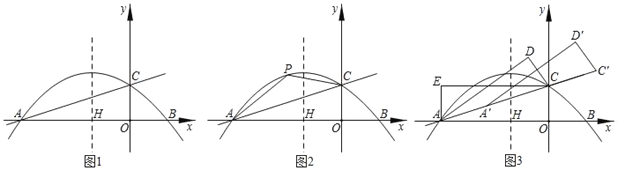
【题目】已知抛物线y=﹣![]() x2﹣
x2﹣![]() x+2与x轴交于点A,B两点,交y轴于C点,抛物线的对称轴与x轴交于H点,分别以OC、OA为边作矩形AECO.
x+2与x轴交于点A,B两点,交y轴于C点,抛物线的对称轴与x轴交于H点,分别以OC、OA为边作矩形AECO.
(1)求直线AC的解析式;
(2)如图2,P为直线AC上方抛物线上的任意一点,在对称轴上有一动点M,当四边形AOCP面积最大时,求|PM﹣OM|的最大值.
(3)如图3,将△AOC沿直线AC翻折得△ACD,再将△ACD沿着直线AC平移得△A'C′D'.使得点A′、C'在直线AC上,是否存在这样的点D′,使得△A′ED′为直角三角形?若存在,请求出点D′的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
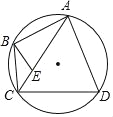
【题目】如图,四边形ABCD为圆内接四边形,A为弧BD中点,连接对角线AC,E在AC上,且AE=AB求证:
(1)∠CBE=![]() ∠CAD;
∠CAD;
(2)AC2=BCCD+AB2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽和小华想利用摸球游戏决定谁去参加市里举办的书法比赛,游戏规则是:在一个不透明的袋子里装有除数字外完全相同的4个小球,上面分别标有数字2,3,4,5.一人先从袋中随机摸出一个小球,另一人再从袋中剩下的3个小球中随机摸出一个小球.若摸出的两个小球上的数字和为偶数,则小丽去参赛;否则小华去参赛.
(1)用列表法或画树状图法,求小丽参赛的概率.
(2)你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com