
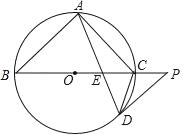
【题目】如图,已知BC是⊙O的直径,点A,D在⊙O上,∠B=2∠CAD,在BC的延长线上有一点P,使得∠P=∠ACB,弦AD交直径BC于点E.
(1)求证:DP与⊙O相切;
(2)判断△DCE的形状,并证明你的结论;
(3)若CE=2,DE=![]() ,求线段BC的长度.
,求线段BC的长度.
【答案】(1)证明见解析;(2)△DCE是等腰三角形,证明见解析;(3)10.
【解析】
(1)连接OD,根据圆周角定理得到∠DOP=2∠DAC,等量代换得到∠COD=∠B,根据圆周角定理得到∠BAC=90°,根据切线的判定定理即可得到结论;
(2)根据圆周角定理和三角形的内角和即可得到结论;
(3)根据相似三角形的性质得到![]() ,于是得到OC=
,于是得到OC=![]() =5,即可得到结论.
=5,即可得到结论.
(1)连接OD,

∴∠DOP=2∠DAC,
∵∠B=2∠CAD,
∴∠COD=∠B,
∵∠P=∠ACB,
∴∠ODP=∠BAC,
∵BC是⊙O的直径,
∴∠BAC=90°,
∴∠ODP=90°,
∴DP与⊙O相切;
(2)△DCE是等腰三角形,
理由:∵∠B=∠COD,∠BOD=180°﹣∠COD,∠BAD+∠AEB=180°﹣∠B,
∴∠BOD=∠BAD+∠AEB,
∵∠BAD=![]() ∠BOD,
∠BOD,
∴∠AEB=![]() ∠BOD,
∠BOD,
∴∠BAD=∠AEB,
∵∠DCE=∠BAE,∠CED=∠AEB,
∴∠CED=∠DCE,
∴△DCE是等腰三角形;
(3)∵OC=OD,
∴∠OCD=∠ODC,
∵DE=DC,
∴∠OCD=∠CED,
∴∠DEC=∠DCE=∠OCD=∠ODC,
∴△DCE∽△OCD,
∴![]() ,
,
∵CE=2,DE=![]() ,
,
∴CD=DE=![]() ,
,
∴OC=![]() =5,
=5,
∴BC=2OC=10.


科目:初中数学 来源: 题型:
【题目】如图,⊙O是梯形ABCD的内切圆,AB∥DC,E、M、F、N分别是边AB、BC、CD、DA上的切点.
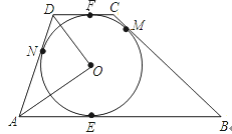
(1)求证:AB+CD=AD+BC
(2)求∠AOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①a,b同号;②当x=1和x=3时,函数值相等;③4a+b=0;④当﹣1<x<5时,y<0.其中正确的有( )
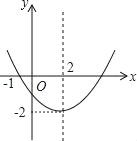
A. ①② B. ②③ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
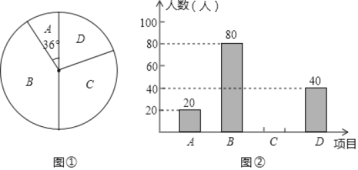
【题目】某学校为了增强学生体质,决定开放以下球类活动项目:A.篮球、B.乒乓球、C.排球、D.足球.为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图(如图①,图②),请回答下列问题:
(1)这次被调查的学生共有多少人?
(2)请你将条形统计图补充完整;
(3)若该校共有学生1900人,请你估计该校喜欢D项目的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,下列结论中,正确结论的有( )个.
①b2﹣4ac>0;②abc>0;③8a+c>0;④9a+3b+c<0.

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
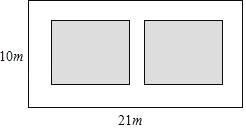
【题目】如图,有一块长为21m、宽为10m的矩形空地,计划在其中修建两块相同的矩形绿地,两块绿地之间及周边留有宽度相等的人行通道,且人行通道的宽度不能超过3米.
(1)如果两块绿地的面积之和为90m2,求人行通道的宽度;
(2)能否改变人行通道的宽度,使得每块绿地的宽与长之比等于3:5,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
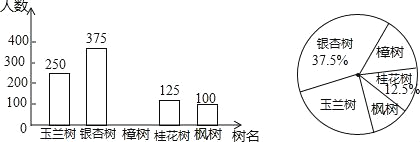
【题目】为积极响应市委政府“加快建设天蓝水碧地绿的美丽长沙”的号召,我市某街道决定从备选的五种树中选购一种进行栽种.为了更好地了解社情民意,工作人员在街道辖区范围内随机抽取了部分居民,进行“我最喜欢的一种树”的调查活动(每人限选其中一种树),并将调查结果整理后,绘制成如图两个不完整的统计图:
请根据所给信息解答以下问题:
(1)这次参与调查的居民人数为: ;
(2)请将条形统计图补充完整;
(3)请计算扇形统计图中“枫树”所在扇形的圆心角度数;
(4)已知该街道辖区内现有居民8万人,请你估计这8万人中最喜欢玉兰树的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正△ABC的顶点B(﹣3,0)、C(﹣1,0),过坐标原点O的一条直线分别与边AB、AC交于点M、N.若OM=2ON,则点N的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商场经销一种高档水果,如果每千克盈利![]() 元,每天可售出
元,每天可售出![]() 千克.经市场调查发现,出售价格每降低
千克.经市场调查发现,出售价格每降低![]() 元,日销售量将增加
元,日销售量将增加![]() 千克.那么每千克应降价多少元,销售该水果每天可获得最大利润?最大利润是多少元?
千克.那么每千克应降价多少元,销售该水果每天可获得最大利润?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com