
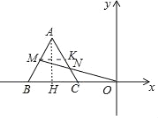
【题目】如图,在平面直角坐标系中,正△ABC的顶点B(﹣3,0)、C(﹣1,0),过坐标原点O的一条直线分别与边AB、AC交于点M、N.若OM=2ON,则点N的坐标为_____.

【答案】![]()
【解析】
作AH⊥BC于H,MK∥BC交AC于点K.由△MKN≌△OCN(AAS),推出MK=OC=1,KN=NC,证明MK是△ABC的中位线即可解决问题;
解:如图,作AH⊥BC于H,MK∥BC交AC于点K.
∵B(﹣3,0)、C(﹣1,0),
∴BC=2,
∵△ABC是等边三角形,
∴AB=AC=BC=2,
∵AH⊥BC,
∴BH=CH=1,
∴AH=![]() ,
,
∴A(﹣2,![]() ),
),
∵OM=2ON,
∴MN=ON,
∵MK∥OB,
∴∠MKN=∠CON,
∵∠MNK=∠CNO,
∴△MKN≌△OCN(AAS),
∴MK=OC=1,KN=NC,
∵MK=![]() BC,MK∥BC,
BC,MK∥BC,
∴MK是△ABC的中位线,
∴AK=CK,
∴K![]() ,
,
∵KN=CN,
∴N![]() ,
,
故答案为![]() .
.


科目:初中数学 来源: 题型:
【题目】(12分)如图,△ABC内接于⊙O,AB=AC,BD为⊙O的弦,且AB∥CD,过点A作⊙O的切线AE与DC的延长线交于点E,AD与BC交于点F.
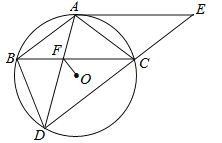
(1)求证:四边形ABCE是平行四边形;
(2)若AE=6,CD=5,求OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
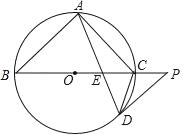
【题目】如图,已知BC是⊙O的直径,点A,D在⊙O上,∠B=2∠CAD,在BC的延长线上有一点P,使得∠P=∠ACB,弦AD交直径BC于点E.
(1)求证:DP与⊙O相切;
(2)判断△DCE的形状,并证明你的结论;
(3)若CE=2,DE=![]() ,求线段BC的长度.
,求线段BC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣![]() x2﹣
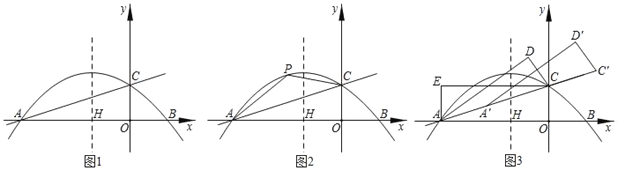
x2﹣![]() x+2与x轴交于点A,B两点,交y轴于C点,抛物线的对称轴与x轴交于H点,分别以OC、OA为边作矩形AECO.
x+2与x轴交于点A,B两点,交y轴于C点,抛物线的对称轴与x轴交于H点,分别以OC、OA为边作矩形AECO.
(1)求直线AC的解析式;
(2)如图2,P为直线AC上方抛物线上的任意一点,在对称轴上有一动点M,当四边形AOCP面积最大时,求|PM﹣OM|的最大值.
(3)如图3,将△AOC沿直线AC翻折得△ACD,再将△ACD沿着直线AC平移得△A'C′D'.使得点A′、C'在直线AC上,是否存在这样的点D′,使得△A′ED′为直角三角形?若存在,请求出点D′的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数m、n,定义一种运算“※”为:m※n=mn+n.
(1)求2※5与2※(﹣5)的值;
(2)如果关于x的方程x※(a※x)=﹣![]() 有两个相等的实数根,求实数a的值.
有两个相等的实数根,求实数a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
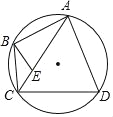
【题目】如图,四边形ABCD为圆内接四边形,A为弧BD中点,连接对角线AC,E在AC上,且AE=AB求证:
(1)∠CBE=![]() ∠CAD;
∠CAD;
(2)AC2=BCCD+AB2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某小组同学为了测量对面楼AB的高度,分工合作,有的组员测得两楼间距离为40米,有的组员在教室窗户处测得楼顶端A的仰角为30°,底端B的俯角为10°,请你根据以上数据,求出楼AB的高度.(精确到0.1米)
(参考数据:sin10°≈0.17, cos10°≈0.98, tan10°≈0.18, ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总数排列名次,在规定时间内每人踢100个以上(含100个)为优秀,下表是成绩最好的甲、乙两班各5名学生的比赛数据.(单位:个)
1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
甲班 | 89 | 100 | 96 | 118 | 97 | 500 |
乙班 | 100 | 96 | 110 | 90 | 104 | 500 |
统计发现两班总数相等,此时有人建议,可以通过考查数据中的其他信息来评判.试从两班比赛数据的中位数、方差、优秀率三个方面考虑,你认为应该选定哪一个班为冠军?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com