练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】二次函数y＝ax2+bx+c（a≠0）的图象如图，下列结论中，正确结论的有（　　）个．

    ①b2﹣4ac＞0；②abc＞0；③8a+c＞0；④9a+3b+c＜0．

    A. 1 B. 2 C. 3 D. 4

    【答案】D

    【解析】

    试题二次函数y=ax2+bx+c（a≠0）的图象如图所示，从图形来看二次函数与X轴有两个交点，那么方程有两个不相等的实数根，所以，即2-4ac＞0，所以①正确；从图象来看，二次函数的图象开口向上，所以a>0，对称轴在y轴的右边，所以，解得b<0;二次函数y=ax2+bx+c与y轴的交点在其负半轴，那么，即c<0，所以abc＞0，所以②正确；从图象来看，二次函数与X轴有两个交点，一个交点在-2、-1之间，即在-2这点二次函数的函数值大于0，所以，即，因为二次函数y=ax2+bx+c（a≠0）的对称轴为-1，即，那么2a=-b,所以-2b=4a，所以，因此③8a+c＞0正确；因为二次函数y=ax2+bx+c（a≠0）的对称轴为-1，-2点关于对称轴x=-1的对称点是3，所以二次函数在-3点的函数值也大于0，所以9a+3b+c＜0，所以全部正确

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某校初三（1）班部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动，收集整理数据后，老师将减压方式分为五类，并绘制了图1、图2两个不完整的统计图，请根据图中的信息解答下列问题．

    （1）初三（1）班接受调查的同学共有多少名；

    （2）补全条形统计图，并计算扇形统计图中的“体育活动C”所对应的圆心角度数；

    （3）若喜欢“交流谈心”的5名同学中有三名男生和两名女生；老师想从5名同学中任选两名同学进行交流，直接写出选取的两名同学都是女生的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知AD是△ABC的中线， DE⊥AB于E， DF⊥AC于F， 且BE=CF， 求证：(1)AD是∠BAC的平分线；(2)AB=AC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

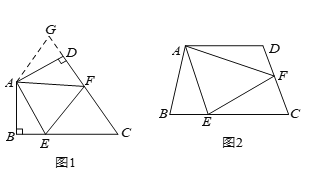
    【题目】如图（），在四边形中，，，，，分别是，上的点，且．探究图中线段，，之间的数量关系．小王同学探究此问题的方法是，延长到点，使，连接，先证明≌，再证明≌，可得出结论，他的结论应该是__________．

    如图（），若在四边形中，，，，分别是,上的点，且，上述结论是否仍然成立，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线经过两点，与x轴交于另一点B．点P是抛物线上的动点。

    （1）求抛物线的解析式；

    （2）是否存在点P，使得△BCP是以BC为直角边的直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，说明理由；

    （3）当P运动到第一象限时，过P作直线PM平行y轴，交直线BC于点M。

    ①求线段PM长度的最大值

    ②D为平面内任意一点，当线段PM最大时，是否存在以C、P、M、D为顶点的平行四边形。若存在，直接写出所有符合条件的点D坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙、丙、丁合作生产一批零件．已知甲生产零件的数量是乙生产零件的数量的，乙生产零件的数量是丙生产零件的数量的倍，丁比甲多生产了个零件，设丙生产零件个．

    （1）则乙生产零件 个，丁生产零件 个；

    （2）若乙生产的零件数量比丁多，用含的代数式表示出乙比丁多生产零件的个数；

    （3）若乙和丁生产的零件数量一样多，则这批零件共有多少个？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①所示是一个长为2m，宽为2n的长方形，沿图中虚线用剪刀均分成四个小长方形，然后按图②的方式拼成一个正方形．

    （1）你认为图②中的阴影部分的正方形的边长等于_________________；

    （2）请用两种不同的方法列代数式表示图②中阴影部分的面积．

    方法① __________________．方法② _____________________；

    （3）观察图②，你能写出(m+n)2，(m-n)2，mn这三个代数式之间的等量关系吗？

    答：________________________ .

    （4）根据（3）题中的等量关系，解决如下问题：若a+b=6，ab=4，则求(a-b)2的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AD⊥BC，垂足为D，AD=CD，点E在AD上，DE=BD，M、N分别是AB、CE的中点．

    （1）求证：△ADB≌△CDE；

    （2）求∠MDN的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（问题提出）

    学习了三角形全等的判定方法（即“SAS”、“ASA”、“AAS”、“SSS”）和直角三角形全等的判定方法（即“HL”）后，我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究．

    （初步思考）

    我们不妨将问题用符号语言表示为：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，然后，对∠B进行分类，可分为“∠B是直角、钝角、锐角”三种情况进行探究．

    （深入探究）

    第一种情况：当∠B是直角时，△ABC≌△DEF．

    （1）如图①，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E=90°，根据 ，可以知道Rt△ABC≌Rt△DEF．

    第二种情况：当∠B是钝角时，△ABC≌△DEF．

    （2）如图②，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是钝角，求证：△ABC≌△DEF．

    第三种情况：当∠B是锐角时，△ABC和△DEF不一定全等．

    （3）在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是锐角，请你用尺规在图③中作出△DEF，使△DEF和△ABC不全等．（不写作法，保留作图痕迹）

    （4）∠B还要满足什么条件，就可以使△ABC≌△DEF？请直接写出结论：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是锐角，若 ，则△ABC≌△DEF．

    查看答案和解析>>

    同步练习册答案