
【题目】如图,抛物线![]() 经过
经过![]() 两点,与x轴交于另一点B.点P是抛物线上的动点。
两点,与x轴交于另一点B.点P是抛物线上的动点。
(1)求抛物线的解析式;
(2)是否存在点P,使得△BCP是以BC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)当P运动到第一象限时,过P作直线PM平行y轴,交直线BC于点M。
①求线段PM长度的最大值
②D为平面内任意一点,当线段PM最大时,是否存在以C、P、M、D为顶点的平行四边形。若存在,直接写出所有符合条件的点D坐标.

【答案】(1) ![]() ;(2)见解析;(3) ①4; ②D1
;(2)见解析;(3) ①4; ②D1![]() ,D2
,D2 ![]() ,D3
,D3![]() .
.
【解析】分析: (1)把![]() 两点代入
两点代入![]() 求出抛物线解析式;
求出抛物线解析式;
(2)先确定B(4,0),则判断△OBC为等腰直角三角形得到∠OBC=∠OCB=45°,设![]() 第一种情况,当以C为直角顶点时,过点P作PT⊥y轴,利用TC=TP,可列方程
第一种情况,当以C为直角顶点时,过点P作PT⊥y轴,利用TC=TP,可列方程![]() ,即可求得满足条件的P点坐标;第二种情况,当以B为直角顶点时,过点P作PH⊥x轴,可得PH=HB,从而
,即可求得满足条件的P点坐标;第二种情况,当以B为直角顶点时,过点P作PH⊥x轴,可得PH=HB,从而![]() , 即可求得满足条件的P点坐标;
, 即可求得满足条件的P点坐标;
(3)①求出直线BC解析式, 根据PM平行y轴用二次函数表示P M的长度从而表示出PM的最大值;
②分3种情况:CM为对角线;MP为对角线;CP为对角线.
详解:
(1)将![]() 两点代入到
两点代入到![]() 中得,
中得,
![]()
∴抛物线的解析式为![]() .
.
(2) 存在.
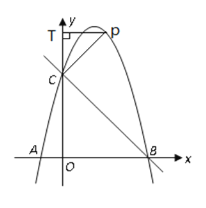
第一种情况,当以C为直角顶点时,过点P作PT⊥y轴,垂足为T。
由抛物线的解析式可得B点坐标为(4,0)
∴OB=OC,∠BOC =90°
∴∠OCB=∠OBC=45°.
∵∠BCP=90°,
∴∠TCP =45°=∠C PT.
∴TC=TP
设![]()
即:![]() ,
,
解得:![]() (舍去),
(舍去),![]() .
.
∴![]()
则P1的坐标是![]() .
.
第二种情况,当以B为直角顶点时,
过点P作PH⊥x轴,垂足为H./span>∵∠CBA=45°,∠CBP=90°,
∴∠OBP=45°.∴∠HPB=45°,
∴PH=HB.
即:![]() ,
,
解得:![]() (舍去),
(舍去),![]() .
.
∴![]()
则P2的坐标是![]() .
.
综上所述,P的坐标是![]() 或
或![]()

(3)① ∵B(4,0), ![]() ∴直线BC解析式为
∴直线BC解析式为![]()
又∵PM平行y轴,设![]()
∴M![]() 。
。
则P M =![]() =
=![]()
∴线段PM长度的最大值为4.
②D1![]() ,D2
,D2 ![]() ,D3
,D3![]()



科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为6cm,B为⊙O外一点,OB交⊙O于点A,AB=OA,动点P从点A出发,以π cm/s的速度在⊙O上按逆时针方向运动一周回到点A立即停止.当点P运动的时间为______时,BP与⊙O相切.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两城市之间开通了动车组高速列车.已知每隔2h有一列速度相同的动车组列车从甲城开往乙城.如图,OA是第一列动车组列车离开甲城的路程s(km)与运行时间t(h)的函数图象,BC是一列从乙城开往甲城的普通快车距甲城的路程s(km)与运行时间t(h)的函数图象.请根据图中的信息,解答下列问题:
(1)从图象看,普通快车发车时间比第一列动车组列车发车时间 1h(填”早”或”晚”),点B的纵坐标600的实际意义是 ;
(2)请直接在图中画出第二列动车组列车离开甲城的路程s(km)与时间t(h)的函数图象;
(3)若普通快车的速度为100km/h,
①求第二列动车组列车出发多长时间后与普通快车相遇?
②请直接写出这列普通快车在行驶途中与迎面而来的相邻两列动车组列车相遇的时间间隔.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展了为期一个月的“热爱劳动”教育,为了了解学生受教育后的效果,随机调查了部分家长,对学生周末家务劳动时间(单位:分钟)进行统计,按家务劳动时间分
A、B、C、D、E、F六个等级,绘制了如图8所示的不完整的统计图表:


请根据图表中提供的信息,解答下面的问题:
(1)这次一共调査了 位家长,家务劳动时间统计表中的b = ;
(2)请把家务劳动时间条形统计图补充完整;
(3)若绘制“家务劳动时间扇形统计图”,等级为“D”所对应扇形的圆心角是 度;
(4)若该中学有3000名学生,估计周末家务劳动时间在40分钟以上的学生有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有![]() 筐白菜,以每筐
筐白菜,以每筐![]() 千克为标准,超过或不足的分别用正、负来表示,记录如下:
千克为标准,超过或不足的分别用正、负来表示,记录如下:
与标准质量的差 |
|
|
|
|
|
|
筐 数 |
|
|
|
|
|
|
(1)与标准质量比较,![]() 筐白菜总计超过或不足多少千克?
筐白菜总计超过或不足多少千克?
(2)若白菜每千克售价![]() 元,则出售这
元,则出售这![]() 筐白菜可卖多少元?
筐白菜可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,下列结论中,正确结论的有( )个.
①b2﹣4ac>0;②abc>0;③8a+c>0;④9a+3b+c<0.

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径点F、C是半圆弧ABC上的三等份点,连接AC,AF,过点C作CD⊥AF交AF的延长线于点D,垂足为D.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为4,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在∠△ACB和△DCE中,AC=BC,CD=CE,∠ACB=∠DCE=90°,连接AE、BD交于点O,AE与DC交于点M,BD与AC交于点N.

(1)试判断AE、BD之间的关系,并说明理由;
(2)连接CO,则下面两个结论中选择你认为正确的一个加以说明①射线CO平分∠ACD ②射线OC平分∠BOE
查看答案和解析>>
科目:初中数学 来源: 题型:
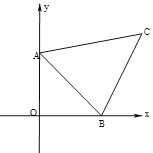
【题目】如图,在平面直角坐标系中,A(0,3),B(3,0),C(5,4),∠OAB=∠OBA=45°,点P为坐标系中第一象限内一点(不与C重合),若△BAP≌△ABC,则点P坐标为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com