
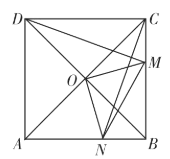
【题目】如图,正方形ABCD的对角线AC与BD相交于点O.将∠COB绕点O顺时针旋转,设旋转角为α(0<α<90°),角的两边分别与BC,AB交于点M,N,连接DM,CN,MN,下列四个结论:①∠CDM=∠COM;②CN⊥DM;③△CNB≌△DMC;④AN2+CM2=MN2;其中正确结论的个数是( )
A. 1B. 2C. 3D. 4
【答案】C
【解析】
利用正方形的性质进行等角转换,正方形ABCD的对角线AC与BD相交于点O,AC⊥BD,∠COM+∠MOB=∠BON+∠MOB=90°,∠COM=∠BON,OB=OC,∠OBN=∠OCM=45°,△ONB≌△OMC,得NB=MC,又BC=CD,∠DCM=∠CBN=90°,故△CNB≌△DMC
解:∵正方形ABCD的对角线AC与BD相交于点O
∴AC⊥BD,∠COM+∠MOB=∠BON+∠MOB=90°
∴∠COM=∠BON,OB=OC,∠OBN=∠OCM=45°
∴△ONB≌△OMC
∴NB=MC
又∵BC=CD,∠DCM=∠CBN=90°
∴△CNB≌△DMC
∴③结论正确;
由△CNB≌△DMC,得出∠BCN=∠CDM
又∠CDM+∠CMD=90°
∴∠BCN+∠CMD=90°
∴CN⊥DM
故②结论正确.


科目:初中数学 来源: 题型:
【题目】如图,函数y=x的图象与函数y=![]() (x>0)的图象相交于点P(2,m).
(x>0)的图象相交于点P(2,m).
(1)求m,k的值;
(2)直线y=4与函数y=x的图象相交于点A,与函数y=![]() (x>0)的图象相交于点B,求线段AB长.
(x>0)的图象相交于点B,求线段AB长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山地自行车越来越受到中学生的喜爱,各种品牌相继投放市场,某车行经营的A型车去年销售总额为5万元,今年每辆销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.
(1)今年A型车每辆售价多少元?(用列方程的方法解答)
(2)该车行计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A,B两种型号车的进货和销售价格如下表:
A型车 | B型车 | |
进货价格(元) | 1100 | 1400 |
销售价格(元) | 今年的销售价格 | 2000 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场欲购进果汁饮料和碳酸饮料共50箱,果汁饮料毎箱进价为55元,售价为63元;碳酸饮料毎箱进价为36元,售价为42元;设购进果汁饮料x箱(x为正整数),且所购进的两种饮料能全部卖出,获得的总利润为W元(注,总利润=总售价﹣总进价),
(1)设商场购进碳酸饮料y箱,直接写出y与x的函数关系式;
(2)求总利润W关于x的函数关系式;
(3)如果购进两种饮料的总费用不超过2000元,那么该商场如何进货才能获利最多?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
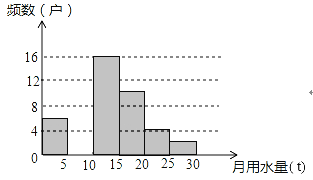
【题目】八年级(1)班同学为了解某小区家庭月均用水情况,随机调査了该小区部分家庭,并将调查数据整理成如下两幅不完整的统计图表:
月均用水量x(t) | 频数(户) | 频率 |
0<x≤5 | 6 | 0.12 |
5<x≤10 | m | 0.24 |
10<x≤15 | 16 | 0.32 |
15<x≤20 | 10 | 0.20 |
20<x≤25 | 4 | n |
25<x≤30 | 2 | 0.04 |
请根据以上信息,解答以下问题:
(1)直接写出频数分布表中的m、n的值并把频数直方图补充完整;
(2)求出该班调查的家庭总户数是多少?
(3)求该小区用水量不超过15的家庭的频率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[x]表示不超过x的最大整数.如,[π]=3,[2]=2,[﹣2.1]=﹣3.则下列结论:
①[﹣x]=﹣[x];
②若[x]=n,则x的取值范围是n≤x<n+1;
③当﹣1<x<1时,[1+x]+[1﹣x]的值为1或2;
④x=﹣2.75是方程4x﹣2[x]+5=0的唯一一个解.
其中正确的结论有_____(写出所有正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A9m,0、Bm,0m0,以AB为直径的⊙M交y轴正半轴于点C,CD是⊙M的切线,交x轴正半轴于点D,过A作AECD于E,交⊙于F.
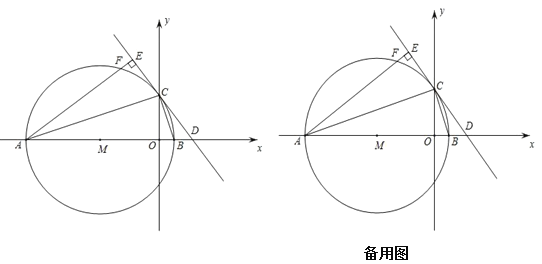
(1)求C的坐标;(用含m的式子表示)
(2)①请证明:EFOB;②用含m的式子表示AFC的周长;
(3)若![]() ,
,![]() ,
,![]() 分别表示
分别表示![]() 的面积,记
的面积,记![]() ,对于经过原点的二次函数
,对于经过原点的二次函数![]() ,当
,当![]() 时,函数y的最大值为a,求此二次函数的解析式.
时,函数y的最大值为a,求此二次函数的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com