
【题目】某商场欲购进果汁饮料和碳酸饮料共50箱,果汁饮料毎箱进价为55元,售价为63元;碳酸饮料毎箱进价为36元,售价为42元;设购进果汁饮料x箱(x为正整数),且所购进的两种饮料能全部卖出,获得的总利润为W元(注,总利润=总售价﹣总进价),
(1)设商场购进碳酸饮料y箱,直接写出y与x的函数关系式;
(2)求总利润W关于x的函数关系式;
(3)如果购进两种饮料的总费用不超过2000元,那么该商场如何进货才能获利最多?并求出最大利润.
【答案】(1)y=50﹣x;(2)W=2x+300;(3)当x=10时,W有最大值,最大值为320
【解析】分析:(1)根据两种饮料共50箱,即可得出y与x之间的函数关系式;
(2)根据总利润=总售价-总进价,总价=单价×数量列出关系式即可;
(3)根据购进两种饮料的总费用不超过2000元列出不等式求得x的取值范围,然后根据一次函数的性质和增减性即可得出答案.
详解:(1)y与x之间的函数关系式为y=50﹣x;
(2)W=(63﹣55)x+(42﹣36)(50﹣x),整理得:W=2x+300;
(3)根据题意得:55x+36(50﹣x)≤2000
整理得:19x≤200.
∴x≤10![]() .
.
∴x的最大值为10.
又∵W=2x+300,W随着x的增大而增大.
∴当x=10时,W有最大值,最大值为320.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】对于一个函数,如果它的自变量 x 与函数值 y 满足:当1≤x≤1 时,1≤y≤1,则称这个函数为“闭 函数”.例如:y=x,y=x 均是“闭函数”. 已知 y ax2 bx c(a0) 是“闭函数”,且抛物线经过点 A(1,1)和点 B(1,1),则 a 的取值范围是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a,b,c在数轴上的位置如图所示,且表示数a的点、数b的点与原点的距离相等.
(1)用“>”“<”或“=”填空:b______0,a+b______0,a-c______0,b-c______0;
(2)|b-1|+|a-1|=________;
(3)化简:|a+b|+|a-c|-|b|+|b-c|.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 下图是某学校全体教职工年龄的频数分布直方图(统计中采用“上限不在内”的原则,如年龄为36岁统计在36≤x<38小组,而不在34≤x<36小组),根据图形提供的信息,下列说法中错误的是
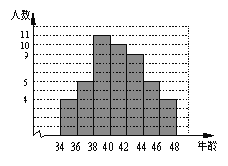
A.该学校教职工总人数是50人
B.年龄在40≤x<42小组的教职工人数占该学校总人数的20%
C.教职工年龄的中位数一定落在40≤x<42这一组
D.教职工年龄的众数一定在38≤x<40这一组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线AC与BD相交于点O.将∠COB绕点O顺时针旋转,设旋转角为α(0<α<90°),角的两边分别与BC,AB交于点M,N,连接DM,CN,MN,下列四个结论:①∠CDM=∠COM;②CN⊥DM;③△CNB≌△DMC;④AN2+CM2=MN2;其中正确结论的个数是( )
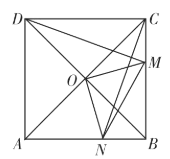
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
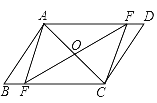
【题目】如图所示,AC是ABCD的一条对角线,过AC中点O的直线EF分别交AD,BC于点E,F.
(1)求证:△AOE≌△COF;
(2)连接AF和CE,当EF⊥AC时,判断四边形AFCE的形状,并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:(直接写出结果)
(1)﹣6﹣(﹣12)= ;
(2)﹣10﹣(+8)= ;
(3)﹣15+15= ;
(4)9﹣(+13)= ;
(5)(﹣![]() )÷(﹣4)×(﹣10)= ;
)÷(﹣4)×(﹣10)= ;
(6)﹣(﹣6)2= ;
(7)﹣12×(﹣2)3= ;
(8)﹣16÷(![]() )= ;
)= ;
(9)![]() ×0= ;
×0= ;
(10)![]() = ;
= ;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.
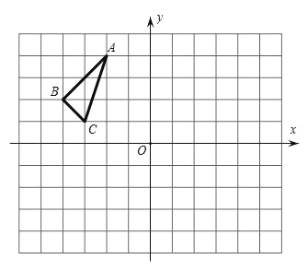
(1)画出ABC关于原点O的中心对称图形A1B1C1,并写出点A1的坐标;
(2)将ABC绕点C顺时针旋转90得到A2B2C,画出A2B2C,求在旋转过程中,线段CA所扫过的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com