练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

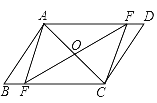
    【题目】如图所示，AC是ABCD的一条对角线，过AC中点O的直线EF分别交AD，BC于点E，F．

    （1）求证：△AOE≌△COF；

    （2）连接AF和CE，当EF⊥AC时，判断四边形AFCE的形状，并说明理由

    【答案】（1）详见解析；（2）是菱形;

    【解析】

    根据菱形判定定理：对角线互相垂直且平分的四边形是菱形

    （1） 证明：∵四边形ABCD是平行四边形，

    ∴AD∥BC，∴∠EAO=∠FCO，

    ∵O是OA的中点，

    ∴OA=OC，

    在△AOE和△COF中，∠EAO=∠FCOOA=OC∠AOE=∠COF，

    ∴△AOE≌△COF（ASA）；

    （2） EF⊥AC时，四边形AFCE是菱形；

    由（1）中△AOE≌△COF，得

    AE=CF，OE=OF，

    又∵OA=OC，EF⊥AC

    ∴四边形AFCE是菱形.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】现有20箱苹果，以每箱25千克为标准，超过的千克数用正数表示，不足的千克数用负数表示，结果记录如表：

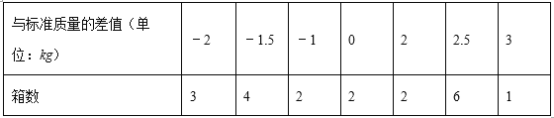
    （1）20箱苹果中，最重的一箱比最轻的一箱重　 　kg；

    （2）与标准质量相比，20箱苹果总计超过或不足多少千克？

    （3）若苹果每千克售价12元，则售出这20箱苹果可获得多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（背景知识）

    数轴是初中数学的一个重要工具，利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律：若数轴上点、点表示的数分别为、，则、两点之间的距离，线段的中点表示的数为.

    （问题情境）

    如图，数轴上点表示的数为，点表示的数为8，点从点出发，以每秒3个单位长度的速度沿数轴向右匀速运动，同时点从点出发，以每秒2个单位长度的速度向左匀速运动，设运动时间为秒（）.

    （综合运用）

    （1）填空：

    ①、两点之间的距离________，线段的中点表示的数为__________.

    ②用含的代数式表示：秒后，点表示的数为____________；点表示的数为___________.

    ③当_________时，、两点相遇，相遇点所表示的数为__________.

    （2）当为何值时，.

    （3）若点为的中点，点为的中点，点在运动过程中，线段的长度是否发生变化？若变化，请说明理由；若不变，请求出线段的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商场欲购进果汁饮料和碳酸饮料共50箱，果汁饮料毎箱进价为55元，售价为63元；碳酸饮料毎箱进价为36元，售价为42元；设购进果汁饮料x箱（x为正整数），且所购进的两种饮料能全部卖出，获得的总利润为W元（注，总利润=总售价﹣总进价），

    （1）设商场购进碳酸饮料y箱，直接写出y与x的函数关系式；

    （2）求总利润W关于x的函数关系式；

    （3）如果购进两种饮料的总费用不超过2000元，那么该商场如何进货才能获利最多？并求出最大利润．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，ABCD中，E，F分别是AB，CD的中点，则图中有（　　）个平行四边形．

    A. 7个 B. 8个 C. 9个 D. 10个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】[x]表示不超过x的最大整数．如，[π]=3，[2]=2，[﹣2.1]=﹣3．则下列结论：

    ①[﹣x]=﹣[x]；

    ②若[x]=n，则x的取值范围是n≤x＜n+1；

    ③当﹣1＜x＜1时，[1+x]+[1﹣x]的值为1或2；

    ④x=﹣2.75是方程4x﹣2[x]+5=0的唯一一个解．

    其中正确的结论有_____（写出所有正确结论的序号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我市城市居民用电收费方式有以下两种：

    (甲)普通电价：全天0.53元/度；

    (乙)峰谷电价：峰时(早8:00~晚21:00)0.56元/度；谷时(晚21:00~早8:00)0.36元/度．

    估计小明家下月总用电量为200度，

    ⑴若其中峰时电量为50度，则小明家按照哪种方式付电费比较合适？能省多少元？

    ⑵请你帮小明计算,峰时电量为多少度时，两种方式所付的电费相等?

    ⑶到下月付费时, 小明发现那月总用电量为200度，用峰谷电价付费方式比普通电价付费方式省了14元，求那月的峰时电量为多少度？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】八（1）班同学到野外上数学活动课，为测量池塘两端A、B的距离，设计了如下方案：

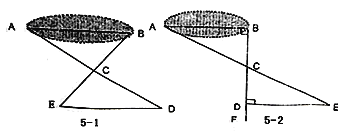
    （Ⅰ）如图5-1，先在平地上取一个可直接到达A、B的点C，连接AC、BC，并分别延长AC至D，BC至E，使DC=AC，EC=BC，最后测出DE的距离即为AB的长；

    （Ⅱ）如图5-2，先过B点作AB的垂线BF，再在BF上取C、D两点使BC=CD,接着过D作BD的垂线DE，交AC的延长线于E，则测出DE的长即为AB的距离.

    阅读后1回答下列问题：

    （1）方案（Ⅰ）是否可行？说明理由.

    （2）方案（Ⅱ）是否可行？说明理由.

    （3）方案（Ⅱ）中作BF⊥AB，ED⊥BF的目的是 ；若仅满足∠ABD=∠BDE≠90°, 方案（Ⅱ）是否成立？ .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某班为满足同学们课外活动的需求，要求购排球和足球若干个．已知足球的单价比排球的单价多30元，用500元购得的排球数量与用800元购得的足球数量相等．

    （1）排球和足球的单价各是多少元？

    （2）若恰好用去1200元，有哪几种购买方案？

    查看答案和解析>>

    同步练习册答案