
【题目】八(1)班同学到野外上数学活动课,为测量池塘两端A、B的距离,设计了如下方案:
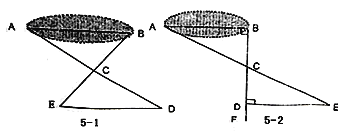
(Ⅰ)如图5-1,先在平地上取一个可直接到达A、B的点C,连接AC、BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测出DE的距离即为AB的长;
(Ⅱ)如图5-2,先过B点作AB的垂线BF,再在BF上取C、D两点使BC=CD,接着过D作BD的垂线DE,交AC的延长线于E,则测出DE的长即为AB的距离.
阅读后1回答下列问题:
(1)方案(Ⅰ)是否可行?说明理由.
(2)方案(Ⅱ)是否可行?说明理由.
(3)方案(Ⅱ)中作BF⊥AB,ED⊥BF的目的是 ;若仅满足∠ABD=∠BDE≠90°, 方案(Ⅱ)是否成立? .
【答案】(1)见解析;(2)见解析;(3)∠ABD=∠BDE=90°,成立.
【解析】
(1)由题意可证明△ACB≌△DCE,AB=DE,故方案(Ⅰ)可行;
(2)由题意可证明△ABC≌△EDC,AB=ED,故方案(Ⅱ)可行;
(3)方案(Ⅱ)中作BF⊥AB,ED⊥BF的目的是∠ABD=∠BDE;若仅满足∠ABD=∠BDE≠90°,仍可以证明△ABC≌△EDC,则也可得到AB=ED.
(1)在△ACB和△DCE中
∵AC=DC
∠ACB=∠DCE
BC=EC
∴△ACB≌△DCE(SAS)
∴AB=DE,
故方案(Ⅰ)可行;
(2)∵CB⊥AB、CD⊥DE
∴∠ABC=∠EDC=90°
在△ABC和△EDC中
∵∠ABC=∠EDC
BC=DC
∠ACB=∠ECD
∴△ABC≌△EDC (ASA)
∴ED=AB,
故方案(Ⅱ)可行;
(3)作BF⊥AB,ED⊥BF的目的是 作∠ABC=∠EDC=90°;
如果∠ABD=∠BDE≠90°,仍可以利用ASA证明△ABC≌△EDC,则也可得到AB=ED.
故答案为:(1)见解析;(2)见解析;(3)∠ABD=∠BDE=90°,成立.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】对于一个函数,如果它的自变量 x 与函数值 y 满足:当1≤x≤1 时,1≤y≤1,则称这个函数为“闭 函数”.例如:y=x,y=x 均是“闭函数”. 已知 y ax2 bx c(a0) 是“闭函数”,且抛物线经过点 A(1,1)和点 B(1,1),则 a 的取值范围是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
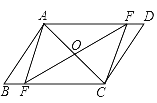
【题目】如图所示,AC是ABCD的一条对角线,过AC中点O的直线EF分别交AD,BC于点E,F.
(1)求证:△AOE≌△COF;
(2)连接AF和CE,当EF⊥AC时,判断四边形AFCE的形状,并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:(直接写出结果)
(1)﹣6﹣(﹣12)= ;
(2)﹣10﹣(+8)= ;
(3)﹣15+15= ;
(4)9﹣(+13)= ;
(5)(﹣![]() )÷(﹣4)×(﹣10)= ;
)÷(﹣4)×(﹣10)= ;
(6)﹣(﹣6)2= ;
(7)﹣12×(﹣2)3= ;
(8)﹣16÷(![]() )= ;
)= ;
(9)![]() ×0= ;
×0= ;
(10)![]() = ;
= ;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )

A. 76° B. 78° C. 80° D. 82°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家规定个人发表文章、出版图书所得稿费的纳税计算方法是:
①稿费不高于800元的不纳税;
②稿费高于800元,而低于4000元的应缴纳超过800元的那部分稿费的14%的税;
③稿费为4000元或高于4000元的应缴纳全部稿费的11%的税.
试根据上述纳税的计算方法作答:
(1)若王老师获得的稿费为2400元,则应纳税 元,若王老师获得的稿费为4000元,则应纳税 元;
(2)若王老师获稿费后纳税420元,求这笔稿费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.
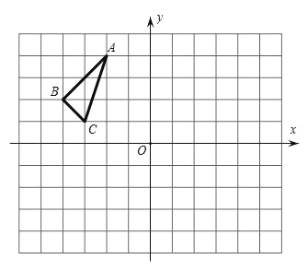
(1)画出ABC关于原点O的中心对称图形A1B1C1,并写出点A1的坐标;
(2)将ABC绕点C顺时针旋转90得到A2B2C,画出A2B2C,求在旋转过程中,线段CA所扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应“弘扬传统文化”的号召,某学校倡导全校1200名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根调查结果绘制成的统计图(部分)如图所示.
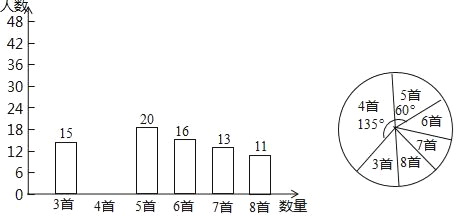
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表
一周诗词诵背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人数 | 10 | 10 | 15 | 40 | 25 | 20 |
请根据调查的信息
(1)活动启动之初学生“一周诗词诵背数量”的中位数为 ;
(2)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
(3)选择适当的统计量,从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com