
【题目】国家规定个人发表文章、出版图书所得稿费的纳税计算方法是:
①稿费不高于800元的不纳税;
②稿费高于800元,而低于4000元的应缴纳超过800元的那部分稿费的14%的税;
③稿费为4000元或高于4000元的应缴纳全部稿费的11%的税.
试根据上述纳税的计算方法作答:
(1)若王老师获得的稿费为2400元,则应纳税 元,若王老师获得的稿费为4000元,则应纳税 元;
(2)若王老师获稿费后纳税420元,求这笔稿费是多少元?
科目:初中数学 来源: 题型:
【题目】如图,函数y=x的图象与函数y=![]() (x>0)的图象相交于点P(2,m).
(x>0)的图象相交于点P(2,m).
(1)求m,k的值;
(2)直线y=4与函数y=x的图象相交于点A,与函数y=![]() (x>0)的图象相交于点B,求线段AB长.
(x>0)的图象相交于点B,求线段AB长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[x]表示不超过x的最大整数.如,[π]=3,[2]=2,[﹣2.1]=﹣3.则下列结论:
①[﹣x]=﹣[x];
②若[x]=n,则x的取值范围是n≤x<n+1;
③当﹣1<x<1时,[1+x]+[1﹣x]的值为1或2;
④x=﹣2.75是方程4x﹣2[x]+5=0的唯一一个解.
其中正确的结论有_____(写出所有正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(1)班同学到野外上数学活动课,为测量池塘两端A、B的距离,设计了如下方案:
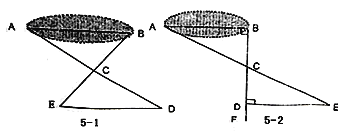
(Ⅰ)如图5-1,先在平地上取一个可直接到达A、B的点C,连接AC、BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测出DE的距离即为AB的长;
(Ⅱ)如图5-2,先过B点作AB的垂线BF,再在BF上取C、D两点使BC=CD,接着过D作BD的垂线DE,交AC的延长线于E,则测出DE的长即为AB的距离.
阅读后1回答下列问题:
(1)方案(Ⅰ)是否可行?说明理由.
(2)方案(Ⅱ)是否可行?说明理由.
(3)方案(Ⅱ)中作BF⊥AB,ED⊥BF的目的是 ;若仅满足∠ABD=∠BDE≠90°, 方案(Ⅱ)是否成立? .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(操作观察)任意一张三角形纸片有3个顶点。
第1次在它的内部增画1个点,此时三角形纸片内部共有1个点;
第2次在它的内部继续增画2个点,此时三角形纸片内部共有1+2=3个点;
第3次在它的内部继续增画3个点,此时三角形纸片内部共有1+2+3=6个点;
……
第![]() 次在它的内部继续增画
次在它的内部继续增画![]() 个点,此时三角形纸片内部共有
个点,此时三角形纸片内部共有![]() 个点。
个点。
(动手实践)
第![]() 次画点后,在三角形纸片内部共有
次画点后,在三角形纸片内部共有![]() 个点,以
个点,以![]() 个点为顶点,把三角形纸片剪成若干个小三角形纸片,设最多可以剪得
个点为顶点,把三角形纸片剪成若干个小三角形纸片,设最多可以剪得![]() 个这样的小三角形。
个这样的小三角形。
(思考解答)
(1)第![]() 次画点后,
次画点后,![]() __________________;(用含有
__________________;(用含有![]() 的代数式表示);
的代数式表示);
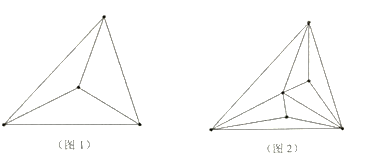
(2)第1次画点后,如图1,以4个点为顶点,将原三角形纸片剪成若干个小三角形,最多可以剪得3个这样的小三角形,所以![]() ;第2次画点后,如图2,以6个点为顶点,最多可以剪得7个这样的小三角形,所以
;第2次画点后,如图2,以6个点为顶点,最多可以剪得7个这样的小三角形,所以![]() ;第3次画点后,以9个点为顶点,可得
;第3次画点后,以9个点为顶点,可得![]() ____________________;
____________________;
(3)第![]() 次画点后,可得
次画点后,可得![]() ______________;(用含有
______________;(用含有![]() 的代数式表示);
的代数式表示);
(4)第![]() 次画点后,可得
次画点后,可得![]() 个小三角形,第
个小三角形,第![]() 次画点后,可得
次画点后,可得![]() 个小三角形,则
个小三角形,则![]() ________________________。(用含有
________________________。(用含有![]() 的代数式表示)。
的代数式表示)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下表,从左到右在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等,则第2019个格子中的数为_________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A9m,0、Bm,0m0,以AB为直径的⊙M交y轴正半轴于点C,CD是⊙M的切线,交x轴正半轴于点D,过A作AECD于E,交⊙于F.
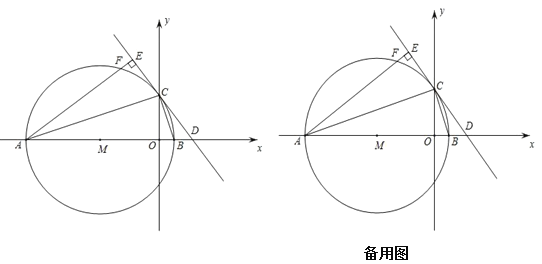
(1)求C的坐标;(用含m的式子表示)
(2)①请证明:EFOB;②用含m的式子表示AFC的周长;
(3)若![]() ,
,![]() ,
,![]() 分别表示
分别表示![]() 的面积,记
的面积,记![]() ,对于经过原点的二次函数
,对于经过原点的二次函数![]() ,当
,当![]() 时,函数y的最大值为a,求此二次函数的解析式.
时,函数y的最大值为a,求此二次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
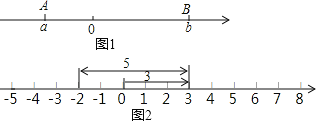
【题目】阅读材料:如图1所示,点A、B在数轴上分别表示有理数a,b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.例如:|5﹣(﹣2)|表示5与﹣2之差的绝对值,实际上也可理解为5与﹣2两数在数轴上所对应的两点之间的距离.
(1)如图2所示,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是﹣2,利用数形结合思想,请参照下图并思考,完成下列各题:
①数轴上表示2与﹣5的两点之间的距离是 个单位长度.
②若数轴上的点A表示的数为x,点B表示的数为﹣1,则A与B两点的距离可以表示为 ;若|x+1|=3,则x为 .
③如果点A表示数﹣1,将A点向右移动18个单位长度,再向左移动13个单位长度终点为B,那么A,B两点间的距离是 .
(2)若数轴上的点A表示的数为x且x为整数,则当x为 时,|x+5|与|x﹣7|的值相等.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com