
����Ŀ����ѧϰ��2��1Բ��ʱ��С������������һ�����⣺��ͼ��1������2����ʾ����ABC�͡�DBC�У���A����D��90�㣮��֤��A��B��C��D�ĵ���ͬһԲ����
С���뵽������֤������ͼ��1������2����ȡBC�е�M������AM��DM������AM��BM��CM��DM��BM��CM����AM��BM��CM��DM������A��B��C��D�ĵ�����MΪԲ�ģ�MBΪ�뾶��Բ����



��������̽������ó��Ľ��ۣ�����������⣺
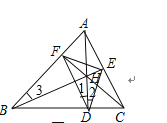
��1����ͼ��3�����ڡ�ABC�У�������AD��BE��CF�ཻ�ڵ�H������DE��DF������BAC��64�㣬���EDF��__________�㣮
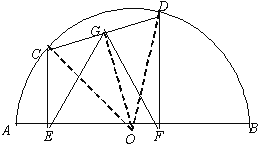
��2����ͼ��4������֪AB����O��ֱ����CD�ǡ�O���ң�GΪCD���е㣬CE��AB��E��DF��AB��F��E��F���غϣ�������EGF��60�㣬��֤��CD��![]() AB��
AB��

���𰸡�52��
����������������� ![]() ��(2)���
��(2)�ã���![]() ��ͬһԲ�ϣ����1=��3.
��ͬһԲ�ϣ����1=��3.
��(2)ͬ���ɵã���![]() ��ͬһԲ�ϣ����EDH=��ECH. ����֤�á�2=��3��
��ͬһԲ�ϣ����EDH=��ECH. ����֤�á�2=��3��
��á�EDF�Ķ���.
![]() ����̽���ó�
����̽���ó�![]() �ĵ���ͬһԲ�ϣ���
�ĵ���ͬһԲ�ϣ���![]() �ĵ���ͬһԲ����
�ĵ���ͬһԲ����
��OGE����OCE����OGF����ODF�� ��OCE����ODF����OGE����OGF����EGF��60����
��һ��֤����COD�ǵȱ����������Ӷ���֤.
��������� ![]() ��ͼ��
��ͼ��
���ı���FBDH��, ![]()
��(2)�ã���![]() ��ͬһԲ�ϣ�
��ͬһԲ�ϣ�
![]()
���ı���![]() ��,
��, ![]()
��(2)ͬ���ɵã���![]() ��ͬһԲ�ϣ�
��ͬһԲ�ϣ�
![]()
![]() ��
��![]()
![]()
![]()
![]()
![]()
��EDF��52����
![]() ֤��������OC��OD��OG��
֤��������OC��OD��OG��
��OC��OD��GΪCD���е㣬��OG��CD��
![]()
![]() ��
��![]()
![]() �ĵ���ͬһԲ�ϣ���
�ĵ���ͬһԲ�ϣ���![]() �ĵ���ͬһԲ����
�ĵ���ͬһԲ����
���OGE����OCE����OGF����ODF��
���OCE����ODF����OGE����OGF����EGF��60����
��Rt��CEO����Rt��DFO��
![]()
![]()
![]()
��![]()
![]() �ǵȱ���������
�ǵȱ���������
![]()
��![]()


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����з���40�䣬��ÿ�䷿�䶨��Ϊ300Ԫ/��ʱ����ȫ��ס����ÿ�䷿�䶨��ÿ����10Ԫ/�죬δ��ס�ķ��佫����1�䣮��ס�ķ����ά����Ϊ20Ԫ/�죬δ��ס�ķ����ά����Ϊ5Ԫ/�죮
��1����ÿ�䷿�䶨��Ϊ360Ԫ/��ʱ����ס�ķ����ж��ټ䣿
��2����ñ���δ��ס�ķ�����x�䣬
����x�Ĵ���ʽ��ʾÿ�䷿��Ķ��ۣ�
�ڵ�ÿ�䷿�䶨��Ϊ����Ԫ/��ʱ���ñ���ÿ�������ɴﵽ11 350Ԫ��������ÿ������룽��ס�ķ��ѣ�ά���ѣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ʽ������ƽ���ʽ�������( )
A. (x+y)(xy)B. (x+y)(xy)C. (x+y)(xy)D. (a+m)(ma)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵������ȷ���ǣ�������
A.����֮������������У��߶����
B.���߾���ֱ��
C.����������ɵ�ͼ�ν�����
D.С��ƽ�ǵĽǿɷ�Ϊ��ǺͶ۽�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������¼��У����ڲ������¼����ǣ�������
A. ������������B. a2��0��a��������
C. �����������ڽǵĺ���180��D. ����˶�Ա�����һ�����а���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ����ʵ���в��ij������ϸ��ֱ��ԼΪ0.00000309�ף���0.00000309�ÿ�ѧ��������ʾΪ��������
A. 3.09��10��6B. 3.09��10��5C. 3.09��106D. 3.09��105
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������2016�����û���ְҵ�䲼����������������飨ְҵ˵����A���������ء����ӣ�B����ҵ��λ��C����ҵ��D������ְҵ�����廧��E��ѧ����F����������ͼ1��ͼ2�Ǹ��ݵ������ݻ��ƶ��ɵIJ�������ͳ��ͼ.�����ͼ���ṩ����Ϣ������������⣺

��1���û�����������û�___________�ˣ�
��2����ͼ.1�У���ȫ����ͳ��ͼ��
��3����ͼ2�У���D���û�����Ӧ���ε�Բ�ĽǶ���Ϊ___________�ȣ�
(4��2016�����û�Լ��7.5���ˣ����ơ�E���û���Լ��________����.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com