
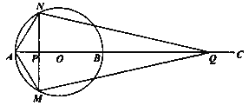
【题目】如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以lcm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为l,设运动时间为t秒.
(1)若AC=5,则当t=时,四边形AMQN为菱形;当t=时,NQ与⊙O相切;
(2)当AC的长为多少时,存在t的值,使四边形AMQN为正方形?请说明理由,并求出此时t的值.
【答案】(1)![]() ,
,![]() ;(2)AC=3,t=1.
;(2)AC=3,t=1.
【解析】
(1)AP=t,CQ=t,则PQ=5-2t,由于NM⊥AB,根据垂径定理得PM=PN,根据菱形的判定方法,当PA=PQ时,四边形AMQN为菱形,即t=5-2t,然后解一元一次方程可求t的值;根据切线的判定定理,当∠ONQ=90时,NQ与⊙O相切,如图,此时OP=t-1,OQ=AC-OA-QC=4-t,再证明Rt△ONP∽Rt△ONQ,利用相似比可得t2-5t+5=0,然后解一元二次方程可得到t的值;
(2)当四边形AMQN为正方形,则∠MAN=90,又可判断AQ为直径,于是得到点P在圆心,所以t=AP=1,CQ=t=1,则得到此时AC=AQ+CQ=3.
(1)![]() ,
,![]() ;
;
(2)当AC的长为3时,存在t=1,使四边形AMQN为正方形.理由如下:
∵四边形AMQN为正方形.
∴∠MAN=90.∴MN为⊙O的直径;
∴MN=AQ=2.∴t=AP=![]() =1,
=1,
又∵CQ=t=1,∴AC=AQ+CQ=2+1=3


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】图,小东在教学楼距地面9米高的窗口C处,测得正前方旗杆顶部A点的仰角为37°,旗杆底部B点的俯角为45°,升旗时,国旗上端悬挂在距地面2.25米处,若国旗随国歌声冉冉升起,并在国歌播放45秒结束时到达旗杆顶端,则国旗应以多少米/秒的速度匀速上升?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店以每件25元的价格购进一批商品,该商品可以自行定价,若每件商品售价a元,则可卖出(400﹣10a)件,但物价局限定每件商品的利润不得超过进价的30%,商店计划要盈利500元,每件商品应定价多少元?需要进货多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等腰直角三角形ABC中,∠ACB=90°,AC=BC=4,D是AB的中点,E,F分别是AC,BC上的点(点E不与端点A,C重合),且AE=CF.
(1)求证:△ADE≌△CDF
(2)如图2连接EF并取EF的中点O,连接DO并延长至点G,使GO=OD,连接DE,DF,GE,GF.求证:四边形EDFG是正方形.
(3)当点E在什么位置时,四边形EDFG的面积最小?直接写出点E的位置及四边形EDFG面积的最小值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=6cm,BC=7cm,∠ABC=30°,点P从A点出发,以1cm/s的速度向B点移动,点Q从B点出发,以2cm/s的速度向C点移动.如果P、Q两点同时出发,经过几秒后△PBQ的面积等于4cm2?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为(4,0),点P是第一象限内直线y=-x+6上一点.O是坐标原点.
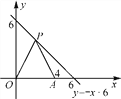
(1)设P(x,y),求△OPA的面积S与x的函数解析式;
(2)当S=10时,求P点的坐标;
(3)在直线y=-x+6上求一点P,使△POA是以OA为底边的等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com