
【题目】某商店以每件25元的价格购进一批商品,该商品可以自行定价,若每件商品售价a元,则可卖出(400﹣10a)件,但物价局限定每件商品的利润不得超过进价的30%,商店计划要盈利500元,每件商品应定价多少元?需要进货多少件?
科目:初中数学 来源: 题型:
【题目】如图①,已知AB是⊙O的直径,点D是线段AB延长线上的一个动点,直线DF垂直于射线AB于点D,当直线DF绕点D逆时针旋转时,与⊙O交于点C,且运动过程中,保持CD=OA
(1)当直线DF与⊙O相切于点C时,求旋转角的度数;
(2)当直线DF与半圆O相交于点C时(如图②),设另一交点为E,连接AE,OC,若AE∥OC.
①AE与OD的大小有什么关系?说明理由.
②求此时旋转角的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我国古代数学著作《九章算术》中记载了这样一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代语言表述为:如图,AB为⊙O的直径,弦CD⊥AB于点E,AE = 1寸,CD = 10寸,求直径AB的长.请你解答这个问题.
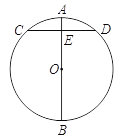
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了分析九年级学生艺术考试的成绩,随机抽查了两个班的各5名学生的成绩,它们分别为:
九(1)班 :96,92,94,97,96;
九(2)班 :90,98,97,98,92.
通过数据分析,列表如下:
班级 | 平均分 | 中位数 | 众数 |
九(1)班 | 95 | a | 96 |
九(2)班 | 95 | 97 | b |
(1)a= , b = ;
(2)计算两个班所抽取的学生艺术成绩的方差,判断哪个班学生的艺术成绩比较稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC内接于以AB为直径的⊙O,过点C作⊙O的切线交BA的延长线于点D,且DA∶AB=1∶2.
(1)求∠CDB的度数;
(2)在切线DC上截取CE=CD,连接EB,判断直线EB与⊙O的位置关系,并证明.
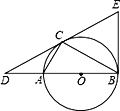
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:
①当x>3时,y<0;②3a+b<0;③﹣1≤a≤﹣![]() ;④4ac﹣b2>8a;
;④4ac﹣b2>8a;
其中正确的结论是( )

A.①③④ B.①②③ C.①②④ D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学生利用业余时间参与了一家网店经营,销售一种成本为30元/件的文化衫,根据以往的销售经验,他整理出这种文化衫的售价y1(元/件),销量y2(件)与第x(1≤x<90)天的函数图象如图所示(销售利润=(售价-成本)×销量).
(1)求y1与y2的函数解析式.
(2)求每天的销售利润W与x的函数解析式.
(3)销售这种文化衫的第多少天,销售利润最大,最大利润是多少?


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以lcm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为l,设运动时间为t秒.
(1)若AC=5,则当t=时,四边形AMQN为菱形;当t=时,NQ与⊙O相切;
(2)当AC的长为多少时,存在t的值,使四边形AMQN为正方形?请说明理由,并求出此时t的值.
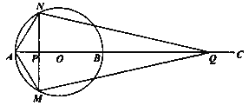
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)如图,两幢建筑物AB和CD,AB⊥BD,CD⊥BD,AB=15cm,CD=20cm,AB和CD之间有一景观池,小南在A点测得池中喷泉处E点的俯角为42°,在C点测得E点的俯角为45°(点B、E、D在同一直线上),求两幢建筑物之间的距离BD(结果精确到0.1m).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
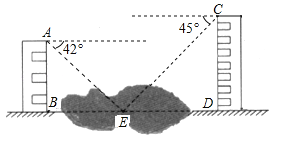
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com