
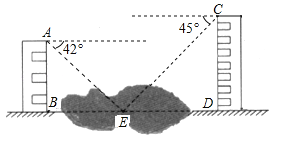
【题目】(6分)如图,两幢建筑物AB和CD,AB⊥BD,CD⊥BD,AB=15cm,CD=20cm,AB和CD之间有一景观池,小南在A点测得池中喷泉处E点的俯角为42°,在C点测得E点的俯角为45°(点B、E、D在同一直线上),求两幢建筑物之间的距离BD(结果精确到0.1m).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某商店以每件25元的价格购进一批商品,该商品可以自行定价,若每件商品售价a元,则可卖出(400﹣10a)件,但物价局限定每件商品的利润不得超过进价的30%,商店计划要盈利500元,每件商品应定价多少元?需要进货多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=6cm,BC=7cm,∠ABC=30°,点P从A点出发,以1cm/s的速度向B点移动,点Q从B点出发,以2cm/s的速度向C点移动.如果P、Q两点同时出发,经过几秒后△PBQ的面积等于4cm2?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为(4,0),点P是第一象限内直线y=-x+6上一点.O是坐标原点.
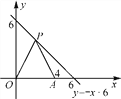
(1)设P(x,y),求△OPA的面积S与x的函数解析式;
(2)当S=10时,求P点的坐标;
(3)在直线y=-x+6上求一点P,使△POA是以OA为底边的等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,且OD=OC.
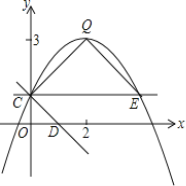
(1)求直线CD的解析式;
(2)求抛物线的解析式;
(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,求证:△CEQ∽△CDO;
(4)在(3)的条件下,若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点P(m,4)在反比例函数y=﹣![]() 的图象上,正比例函数的图象经过点P和点Q(6,n).
的图象上,正比例函数的图象经过点P和点Q(6,n).
(1)求正比例函数的解析式;
(2)求P、Q两点之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一根长为 a 的竹竿 AB 斜靠在墙上,竹竿 AB 的倾斜角为α,当竹竿的顶端 A 下滑到点 A'时,竹竿的另一端 B 向右滑到了点 B',此时倾斜角为β.
(1)线段 AA'的长为_____.
(2)当竹竿 AB 滑到 A'B'位置时,AB 的中点 P 滑到了 P',位置,则点 P 所经过的路线长为___________(两小题均用含 a,α,β的代数式表示)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com