
【题目】如图,一根长为 a 的竹竿 AB 斜靠在墙上,竹竿 AB 的倾斜角为α,当竹竿的顶端 A 下滑到点 A'时,竹竿的另一端 B 向右滑到了点 B',此时倾斜角为β.
(1)线段 AA'的长为_____.
(2)当竹竿 AB 滑到 A'B'位置时,AB 的中点 P 滑到了 P',位置,则点 P 所经过的路线长为___________(两小题均用含 a,α,β的代数式表示)

科目:初中数学 来源: 题型:
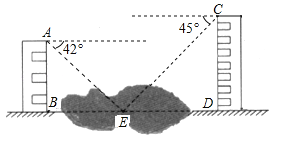
【题目】(6分)如图,两幢建筑物AB和CD,AB⊥BD,CD⊥BD,AB=15cm,CD=20cm,AB和CD之间有一景观池,小南在A点测得池中喷泉处E点的俯角为42°,在C点测得E点的俯角为45°(点B、E、D在同一直线上),求两幢建筑物之间的距离BD(结果精确到0.1m).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
查看答案和解析>>
科目:初中数学 来源: 题型:
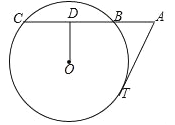
【题目】如图,AT是⊙O的切线,OD⊥BC于点D,并且AT=10cm,AC=20cm,OD=4cm,则半径OC=( )
A. 8.5cm B. 8cm C. 9.5cm D. 9cm
查看答案和解析>>
科目:初中数学 来源: 题型:
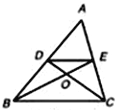
【题目】如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论: ①![]() =
=![]() ; ②
; ②![]() =
=![]() ;③
;③![]() =
=![]() ;④
;④![]() =
=![]() .其中正确的个数有( )
.其中正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
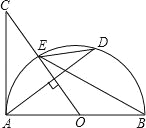
【题目】如图,AB是半圆O的直径,过点O作弦AD的垂线交半圆O于点E,交AC于点C,使∠BED=∠C.
(1)判断直线AC与圆O的位置关系,并证明你的结论;
(2)若AC=8,cos∠BED=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
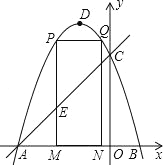
【题目】如图,抛物线 y=﹣x2﹣2x+3 的图象与 x 轴交于 A、B 两点(点 A 在点 B 的左边),与 y轴交于点 C,点 D 为抛物线的顶点.
(1)求点 A、B、C 的坐标;
(2)点 M(m,0)为线段 AB 上一点(点 M 不与点 A、B 重合),过点 M 作 x 轴的垂线,与直线 AC 交于点 E,与抛物线交于点 P,过点 P 作 PQ∥AB 交抛物线于点 Q,过点 Q 作 QN⊥x 轴于点 N,可得矩形 PQNM.如图,点 P 在点 Q 左边,试用含 m 的式子表示矩形 PQNM 的周长;
(3)当矩形 PQNM 的周长最大时,m 的值是多少?并求出此时的△AEM 的面积;
(4)在(3)的条件下,当矩形 PMNQ 的周长最大时,连接 DQ,过抛物线上一点 F 作 y 轴的平行线,与直线 AC 交于点 G(点 G 在点 F 的上方).若 FG=2![]() DQ,求点 F 的坐标.
DQ,求点 F 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(定义)如图1,A,B为直线l同侧的两点,过点A作直线l的对称点![]() ,连接
,连接![]() B交直线l于点P,连接AP,则称点P为点A,B关于直线
B交直线l于点P,连接AP,则称点P为点A,B关于直线![]() 的“等角点”.
的“等角点”.
(运用)如图2,在平面直坐标系xOy中,已知A(2,![]() ),B(-2,-
),B(-2,-![]() )两点.
)两点.
(1)C(4,![]() ),D(4,
),D(4,![]() ),E(4,
),E(4,![]() )三点中,点 是点A,B关于直线x=4的等角点;
)三点中,点 是点A,B关于直线x=4的等角点;
(2)若直线l垂直于x轴,点P(m,n)是点A,B关于直线l的等角点,其中m>2,∠APB=α,求证:![]() ;
;
(3)若点P是点A,B关于直线y=ax+b(a≠0)的等角点,且点P位于直线AB的右下方,当∠APB=60°时,求b的取值范围(直接写出结果).

查看答案和解析>>
科目:初中数学 来源: 题型:
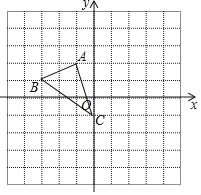
【题目】如图,已知△ABC.
(1)求AC的长;
(2)先将△ABC向右平移2个单位得到△A′B′C′,写出A点的对应点A′的坐标;
(3)再将△ABC绕点C按逆时针方向旋转90°后得到△A1B1C1,写出A点对应点A1的坐标.
(4)求点A到A′所画过痕迹的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
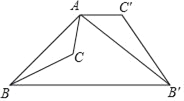
【题目】如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转110°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com