
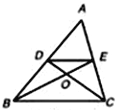
【题目】如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论: ①![]() =
=![]() ; ②
; ②![]() =
=![]() ;③
;③![]() =
=![]() ;④
;④![]() =
=![]() .其中正确的个数有( )
.其中正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
①根据三角形的中位线得出DE∥BC,DE=![]() BC,根据平行线的性质得出相似,根据相似三角形的性质求出即可.
BC,根据平行线的性质得出相似,根据相似三角形的性质求出即可.
②由BE、CD是△ABC的中线,可得DE是△ABC的中位线,然后由三角形中位线的性质,可得△ODE∽△OCB,得出SOCB =4S△ODE.
③由BE、CD是△ABC的中线,可得DE是△ABC的中位线,然后由三角形中位线的性质,可得△ODE∽△OCB,再根据相似三角形的性质求出![]() 即可.
即可.
④由BE、CD是△ABC的中线,得出O是△ABC的重心,根据重心性质可得BO=2OE,△ABC的高=3△BOC的高,且△ABC与△BOC同底(BC)得出S△ABC =3S△BOC,由②和③知,S△ODE= ![]() S△COB,S△ADE =
S△COB,S△ADE = ![]() S△BOC,所以
S△BOC,所以![]() =
=![]() .
.
①∵BE和CD是△ABC的中线,
∴DE=![]() BC,DE∥BC,
BC,DE∥BC,
∴DE:BC=![]() ,△DOE∽△COB,
,△DOE∽△COB,
∴OD:OC=DE:BC=![]() ,
,
故答案①正确.
②∵BE、CD是△ABC的中线,
∴DE∥BC,DE=12BC,AE=EC,
∴△ODE∽△OCB, SOCB =4S△ODE,
∴![]() =
=![]()
故答案②是错的.
③∵BE、CD是△ABC的中线,
∴DE∥BC,DE=![]() BC,AE=EC,AD=DB
BC,AE=EC,AD=DB
∴△ODE∽△OCB,![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() .
.
故答案③正确.
④∵△ABC的中线BE与CD交于点O.∴点O是△ABC的重心,根据重心性质,BO=2OE,△ABC的高=3△BOC的 高,且△ABC与△BOC同底(BC)∴S△ABC =3S△BOC,由②和③知,S△ODE= ![]() S△COB,S△ADE =
S△COB,S△ADE = ![]() S△BOC,∴
S△BOC,∴ ![]() =
=![]() .故④正确.
.故④正确.
综上,①③④正确.故答案选C.


科目:初中数学 来源: 题型:
【题目】如图,ABCD中,E是CD延长线上一点,BE与AD交于点F,CD=2DE,若△DEF的面积为a,则ABCD的面积为( )
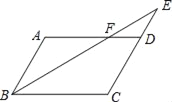
A. 6a B. 8a C. 9a D. 12a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,⊙O是正方形ABCD的外接圆,P是⊙O上不与A、B重合的任意一点,则∠APB等于( )
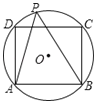
A.45° B.60° C.45° 或135° D.60° 或120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
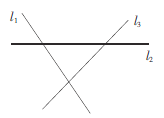
A.一处B.二处C.三处D.四处
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的方程x2+2(m﹣1)x+m2﹣2m﹣3=0(m为实数).
(1)求证:不论m为何值,该方程均有两个不等的实根;
(2)解方程求出两个根x1,x2(x1>x2),并求w=x1(x1+x2)+x12的最值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题6分)甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
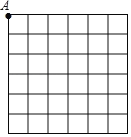
【题目】数学很酷,让我们用理性思维这一利器,去一几何的魔法世界吧.请按要求,完成下面的绘图:作图要求:①仅使用无刻度直尺:②要构造的点必须是格点.
具体要求:
(1)在如图6×6网格中,构造所有等腰三角形,其中个点为A,且一条边长为![]() ;符合条件的三角形有 个,在图上标出.
;符合条件的三角形有 个,在图上标出.
(2)简述构造长度为![]() 的线段的理论依据及计算过程.
的线段的理论依据及计算过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com