练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

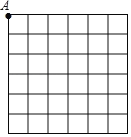
    【题目】数学很酷，让我们用理性思维这一利器，去一几何的魔法世界吧．请按要求，完成下面的绘图：作图要求：①仅使用无刻度直尺：②要构造的点必须是格点．

    具体要求：

    （1）在如图6×6网格中，构造所有等腰三角形，其中个点为A，且一条边长为；符合条件的三角形有　　　　 个，在图上标出．

    （2）简述构造长度为的线段的理论依据及计算过程．

    【答案】（1）5，图形见解析；（2）依据：勾股定理，计算过程：．

    【解析】

    （1）先利用勾股定理计算出的边长，然后利用等腰三角形的定义画三角形即可；

    （2）所依据的是勾股定理，利用勾股定理 即可得出答案．

    （1）有5个等腰三角形(△AEB，△ADC，△AHB，△AFC，△ABC)，如图所示．

    故答案为：5．

    （2）依据：勾股定理，

    因为是在网格中，所以要使两个正整数的平方和为34才可以，只有 才成立

    计算过程：．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

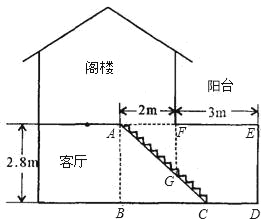
    【题目】汪老师要装修自己带阁楼的新居（下图为新居剖面图），在建造客厅到阁楼的楼梯AC时，为避免上楼时墙角F碰头，设计墙角F到楼梯的竖直距离FG为1.75m．他量得客厅高AB=2.8m，楼梯洞口宽AF=2m．阁楼阳台宽EF=3m．请你帮助汪老师解决下列问题：

    （1）要使墙角F到楼梯的竖直距离FG为1.75m，楼梯底端C到墙角D的距离CD是多少米？

    （2）在（1）的条件下，为保证上楼时的舒适感，楼梯的每个台阶小于20cm，每个台阶宽要大于20cm，问汪老师应该将楼梯建几个台阶？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】．如图，点A、B在⊙O上，直线AC是⊙O的切线，OD⊥OB，连接AB交OC于点D．

    ⑴求证：AC=CD

    ⑵若AC=2，AO=，求OD的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

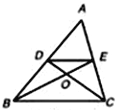
    【题目】如图，在△ABC中，中线BE，CD相交于点O，连接DE，下列结论： ①=； ②=；③=；④=.其中正确的个数有（ ）

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某工厂生产的某种产品按质量分为个档次，生产第一档次（即最低档次）的产品一天生产件，每件利润元，每提高一个档次，利润每件增加元．

    （1）每件利润为元时，此产品质量在第几档次？

    （2）由于生产工序不同，此产品每提高一个档次，一天产量减少件．若生产第档的产品一天的总利润为元（其中为正整数，且≤≤）,求出关于的函数关系式；若生产某档次产品一天的总利润为元，该工厂生产的是第几档次的产品？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】关于函数y=﹣2x+1，下列结论正确的是（　　）

    A. 图象必经过点（﹣2，1） B. 图象经过第一、二、三象限

    C. 当x＞时，y＜0 D. y随x的增大而增大

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线在平面直角坐标系中与轴交于点A，点B（－3，3）也在直线上，将点B先向右平移1个单位长度，再向下平移2个单位长度得到点C，点C也在直线上.

    （1）求点C的坐标和直线的解析式；

    （2）已知直线：经过点B，与轴交于点E，求△ABE的面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中,直线y=-分别与x轴、y轴交于点A、B,且点A的坐标为(8,0),四边形ABCD是正方形．

    （1）填空:b= ；

    （2）求点D的坐标；

    （3）点M是线段AB上的一个动点(点A、B除外),试探索在x上方是否存在另一个点N,使得以O、B、M、N为顶点的四边形是菱形?若不存在,请说明理由;若存在,请求出点N的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于实数a，b，我们可以用min{a，b}表示a，b两数中较小的数，例如min{3，－1}＝－1，min{2，2}＝2. 类似地，若函数y1、y2都是x的函数，则y＝min{y1， y2}表示函数y1和y2的“取小函数”．

    （1）设y1＝x，y2＝，则函数y＝min{x， }的图像应该是 中的实线部分．

    （2）请在下图中用粗实线描出函数y＝min{(x－2)2， (x＋2)2}的图像，并写出该图像的三条不同性质：

    ① ；

    ② ；

    ③ ；

    （3）函数y＝min{(x－4)2， (x＋2)2}的图像关于 对称．

    查看答案和解析>>

    同步练习册答案