
����Ŀ��ij����������ij�ֲ�Ʒ��������Ϊ![]() �����Σ�������һ���Σ�����͵��Σ��IJ�Ʒһ������
�����Σ�������һ���Σ�����͵��Σ��IJ�Ʒһ������![]() ����ÿ������
����ÿ������![]() Ԫ��ÿ���һ�����Σ�����ÿ������
Ԫ��ÿ���һ�����Σ�����ÿ������![]() Ԫ��
Ԫ��
��1��ÿ������Ϊ![]() Ԫʱ���˲�Ʒ�����ڵڼ����Σ�
Ԫʱ���˲�Ʒ�����ڵڼ����Σ�
��2��������������ͬ���˲�Ʒÿ���һ�����Σ�һ���������![]() ������������
������������![]() ���IJ�Ʒһ���������Ϊ
���IJ�Ʒһ���������Ϊ![]() Ԫ������
Ԫ������![]() Ϊ����������
����������![]() ��
��![]() ��
��![]() ��,���
��,���![]() ����
����![]() �ĺ�����ϵʽ��������ij���β�Ʒһ���������Ϊ
�ĺ�����ϵʽ��������ij���β�Ʒһ���������Ϊ![]() Ԫ���ù����������ǵڼ����εIJ�Ʒ��
Ԫ���ù����������ǵڼ����εIJ�Ʒ��
���𰸡���1��ÿ��������16Ԫʱ���˲�Ʒ�������������ڵ��ĵ��Σ�
��2����������Ʒ�������������ڵ�![]() ����ʱ��һ���������
����ʱ��һ���������![]() ��Ԫ����
��Ԫ����
��������ã�
![]()
�����ã�![]()
��������1080ʱ����![]()
��ã�![]() �����������⣬��ȥ��
�����������⣬��ȥ��
�𣺵�������Ʒ�������������ڵ�5����ʱ��һ�������Ϊ1080Ԫ��
����������1��������ɵô˲�Ʒ�����ڵ�4���Σ�
��2����������Ʒ�������������ڵ�x����ʱ��һ���������y�����y��x�ĺ�������ʽ����y=1080�����x��ʵ��ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��AB�ǡ�O��ֱ������P��BA���ӳ����ϣ���CD��AB��E������OD��PC��BC����AOD��2��ABC����P����D����E����GF��BC��Բ��G��F���㣬����CF��BG�������н��ۣ���CD��AB����PC�ǡ�O�����ߣ���OD��GF������CF�����ľ����![]() BG����������ȷ���ǣ�������
BG����������ȷ���ǣ�������
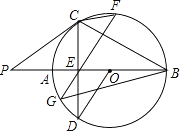
A. �٢ڢ� B. �ۢ� C. �٢ڢ� D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������x�ķ���x2+2��m��1��x+m2��2m��3=0��mΪʵ������
��1����֤������mΪ��ֵ���÷��̾����������ȵ�ʵ����
��2���ⷽ�����������x1��x2��x1��x2��������w=x1��x1+x2��+x12����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
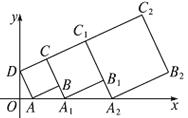
����Ŀ����ƽ��ֱ������ϵ�У�������ABCD��λ����ͼ��ʾ����A������Ϊ(1��0)����D������Ϊ(0��3)���ӳ�CB��x���ڵ�A1����������A1B1C1C���ӳ�C1B1��x���ڵ�A2����������A2B2C2C1�������������Ĺ��ɽ�����ȥ����2017�������ε����Ϊ�� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ�ܿᣬ������������˼ά��һ������ȥһ���ε�ħ������ɣ��밴Ҫ���������Ļ�ͼ����ͼҪ������ʹ���̶�ֱ�ߣ���Ҫ����ĵ�����Ǹ�㣮
����Ҫ��
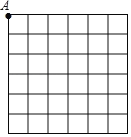
��1������ͼ6��6�����У��������е��������Σ����и���ΪA����һ���߳�Ϊ![]() ���������������������������� ������ͼ�ϱ����
���������������������������� ������ͼ�ϱ����
��2���������쳤��Ϊ![]() ���߶ε��������ݼ�������̣�
���߶ε��������ݼ�������̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ⷽ��
��1��x2+8x��20=0�����䷽����
��2��3x2��6x=1���ù�ʽ����
��3����x��1����x+2��=4
��4����2y��3��2��4��2y��3��+3=0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������ҹ���������������������û����ͽ��������Ϊ���㣮Ϊ�˵���ѧ������������֪ʶ���˽�̶ȣ�ijУ��ѧ��������һ�γ������飬����������Ϊ�ĸ��ȼ���A���dz��˽⣻B���Ƚ��˽⣻C�������˽⣻D�����˽⣮���ݵ���ͳ�ƽ���������˲�����������ͳ��ͼ����
�������˽�̶ȵ�ͳ�Ʊ���
���������˽�̶� | �ٷֱ� |
A���dz��˽� | 5% |
B���Ƚ��˽� | m |
C�������˽� | 45% |
D�����˽� | n |
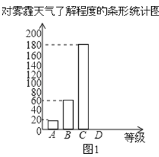
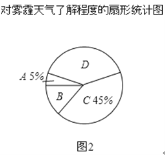
����ͳ��ͼ�����ش��������⣮
��1�����β�������ѧ�������� ���ˣ�m=�� ����n=�� ����
��2��ͼ2��ʾ������ͳ��ͼ��D������������Ӧ��Բ�Ľ����� ���ȣ�
��3���벹ȫ����ͳ��ͼ��
��4�����ݵ�������ѧУ����չ��������֪ʶ������ij��Ҫ�ӡ��dz��˽⡱̬�ȵ�С����С����ѡһ�˲μӣ��������������Ϸ��ȷ������������ǣ����ĸ���ȫ��ͬ��ƹ�����������1��2��3��4��Ȼ��ŵ�һ�������Ĵ��У�һ�����ȴӴ����������һ������һ���ٴ�ʣ�µ����������������һ�������������������ϵ����ֺ�Ϊ��������С��ȥ������С��ȥ��������״ͼ���б���˵�������Ϸ�����Ƿ�ƽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ��Ϊ����ֱ�������Σ�
��Ϊ����ֱ�������Σ�![]()
��1����ͼ1����![]() ��
��![]() �ϣ���
�ϣ���![]() ��
��![]() �غϣ�
�غϣ�![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬���߶�
���е㣬���߶�![]() ��
��![]() ��������ϵ�� ��
��������ϵ�� ��![]() ��
��![]() ����� ��
����� ��
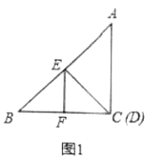
��2����ͼ2����ͼ1�Ļ����ϣ���![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת����ͼ2��λ�ã�����
˳ʱ����ת����ͼ2��λ�ã�����![]() ��һ��ֱ���ϣ�
��һ��ֱ���ϣ�![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬���߶�
���е㣬���߶�![]() ��
��![]() �Ƿ����ij��ȷ����������ϵ��λ�ù�ϵ��֤����Ľ��ۣ�
�Ƿ����ij��ȷ����������ϵ��λ�ù�ϵ��֤����Ľ��ۣ�
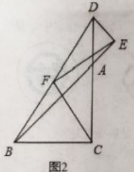
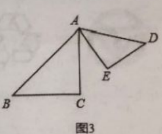
��3����![]() ��
��![]() ����ת����һ���Ƕȵ���ͼ3��λ�ã�
����ת����һ���Ƕȵ���ͼ3��λ�ã�![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬����
���е㣬����![]() ��
��![]() ���������ͼ3�������߶�
���������ͼ3�������߶�![]() ��
��![]() �Ĺ�ϵ����֤����Ľ��ۣ�
�Ĺ�ϵ����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com