
【题目】今年以来,我国持续大面积的雾霾天气让环保和健康问题成为焦点.为了调查学生对雾霾天气知识的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的三种统计图表.
对雾霾了解程度的统计表:
对雾霾的了解程度 | 百分比 |
A.非常了解 | 5% |
B.比较了解 | m |
C.基本了解 | 45% |
D.不了解 | n |
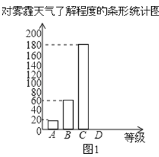
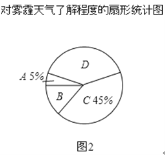
请结合统计图表,回答下列问题.
(1)本次参与调查的学生共有 人,m= ,n= ;
(2)图2所示的扇形统计图中D部分扇形所对应的圆心角是 度;
(3)请补全条形统计图;
(4)根据调查结果,学校准备开展关于雾霾知识竞赛,某班要从“非常了解”态度的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球.若摸出的两个球上的数字和为奇数,则小明去;否则小刚去.请用树状图或列表法说明这个游戏规则是否公平.
【答案】解:(1)400;15%;35%。
(2)126。
(3)∵D等级的人数为:400×35%=140,
∴补全条形统计图如图所示:

(4)列树状图得:
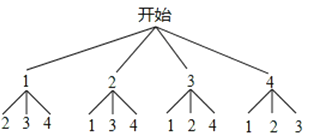
∵从树状图可以看出所有可能的结果有12种,数字之和为奇数的有8种,
∴小明参加的概率为:P(数字之和为奇数)![]() ;
;
小刚参加的概率为:P(数字之和为偶数)![]() 。
。
∵P(数字之和为奇数)≠P(数字之和为偶数),
∴游戏规则不公平。
【解析】(1)根据“基本了解”的人数以及所占比例,可求得总人数:180÷45%=400人。在根据频数、百分比之间的关系,可得m,n的值:![]() 。
。
(2)根据在扇形统计图中,每部分占总体的百分比等于该部分所对应的扇形圆心的度数与360°的比可得出统计图中D部分扇形所对应的圆心角:360°×35%=126°。
(3)根据D等级的人数为:400×35%=140,据此补全条形统计图。
(4)用树状图或列表列举出所有可能,分别求出小明和小刚参加的概率,若概率相等,游戏规则公平;反之概率不相等,游戏规则不公平。


科目:初中数学 来源: 题型:
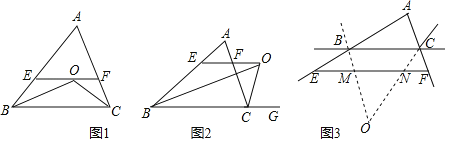
【题目】已知,如图1:![]() 中,
中,![]() 、
、![]() 的平分线相交于点
的平分线相交于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 、
、![]() 于
于![]() 、
、![]()
(1)直接写出图1中所有的等腰三角形.指出![]() 与
与![]() 、
、![]() 间有怎样的数量关系?
间有怎样的数量关系?
(2)在(1)的条件下,若![]() ,
,![]() ,求
,求![]() 的周长;
的周长;
(3)如图2,若![]() 中,
中,![]() 的平分线与三角形外角
的平分线与三角形外角![]() 的平分线
的平分线![]() 交于点
交于点![]() ,过
,过![]() 点作
点作![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,请问(1)中
,请问(1)中![]() 与
与![]() 、
、![]() 间的关系还是否存在,若存在,说明理由:若不存在,写出三者新的数量关系,并说明理由;
间的关系还是否存在,若存在,说明理由:若不存在,写出三者新的数量关系,并说明理由;
(4)如图3,![]() 、
、![]() 的外角平分线的延长线相交于点
的外角平分线的延长线相交于点![]() ,请直接写出
,请直接写出![]() ,
,![]() 、
、![]() ,
,![]() 之间的数量关系.不需证明.
之间的数量关系.不需证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产的某种产品按质量分为![]() 个档次,生产第一档次(即最低档次)的产品一天生产
个档次,生产第一档次(即最低档次)的产品一天生产![]() 件,每件利润
件,每件利润![]() 元,每提高一个档次,利润每件增加
元,每提高一个档次,利润每件增加![]() 元.
元.
(1)每件利润为![]() 元时,此产品质量在第几档次?
元时,此产品质量在第几档次?
(2)由于生产工序不同,此产品每提高一个档次,一天产量减少![]() 件.若生产第
件.若生产第![]() 档的产品一天的总利润为
档的产品一天的总利润为![]() 元(其中
元(其中![]() 为正整数,且
为正整数,且![]() ≤
≤![]() ≤
≤![]() ),求出
),求出![]() 关于
关于![]() 的函数关系式;若生产某档次产品一天的总利润为
的函数关系式;若生产某档次产品一天的总利润为![]() 元,该工厂生产的是第几档次的产品?
元,该工厂生产的是第几档次的产品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 在平面直角坐标系中与
在平面直角坐标系中与![]() 轴交于点A,点B(-3,3)也在直线
轴交于点A,点B(-3,3)也在直线![]() 上,将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,点C也在直线
上,将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,点C也在直线![]() 上.
上.
(1)求点C的坐标和直线![]() 的解析式;
的解析式;
(2)已知直线![]() :
:![]() 经过点B,与
经过点B,与![]() 轴交于点E,求△ABE的面积.
轴交于点E,求△ABE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,等腰梯形ABCD的顶点坐标分别为A(1,1),B(2,﹣1),C(﹣2,﹣1),D(﹣1,1).以A为对称中心作点P(0,2)的对称点P1,以B为对称中心作点P1的对称点P2,以C为对称中心作点P2的对称点P3,以D为对称中心作点P3的对称点P4,…,重复操作依次得到点P1,P2,…,则点P2010的坐标是( )
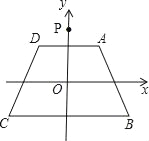
A. (2010,2) B. (2010,﹣2) C. (2012,﹣2) D. (0,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线y=-![]() 分别与x轴、y轴交于点A、B,且点A的坐标为(8,0),四边形ABCD是正方形.
分别与x轴、y轴交于点A、B,且点A的坐标为(8,0),四边形ABCD是正方形.


(1)填空:b= ;
(2)求点D的坐标;
(3)点M是线段AB上的一个动点(点A、B除外),试探索在x上方是否存在另一个点N,使得以O、B、M、N为顶点的四边形是菱形?若不存在,请说明理由;若存在,请求出点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,已知AB=AC,∠BAC=90°,E为边AC上一点,连接BE.
(1)如图1,若∠ABE=15°,O为BE中点,连接AO,且AO=1,求BC的长;
(2)如图2,D为AB上一点,且满足AE=AD,过点A作AF⊥BE交BC于点F,过点F作FG⊥CD交BE的延长线于点G,交AC于点M,求证:BG=AF+FG.
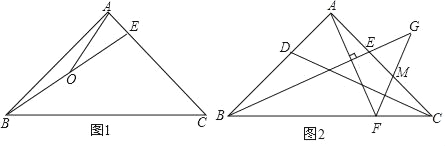
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=mx2﹣2mx﹣3m(m>0)与x轴交于A、B两点,与y轴交于点C,点M为抛物线的顶点,且OC=OB.
(1)求抛物线的解析式.
(2)若抛物线上有一点P,连PC交线段BM于Q点,且S△BPQ=S△CMQ,求P点的坐标.
(3)把抛物线沿x轴正半轴平移n个单位,使平移后的抛物线交直线BC于E、F两点,且E、F关于点B对称,求n的值.
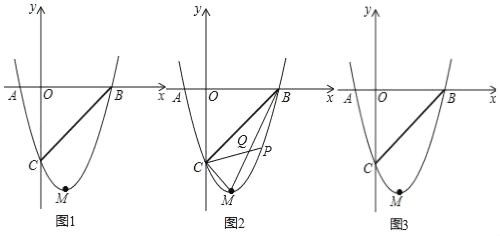
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组在研究函数y=![]() x3﹣2x的图象与性质时,已列表、描点并画出了图象的一部分.
x3﹣2x的图象与性质时,已列表、描点并画出了图象的一部分.
x | … | ﹣4 | ﹣3.5 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 3.5 | 4 | … |
y | … | ﹣ | ﹣ |
|
|
| 0 | ﹣ | ﹣ | ﹣ |
|
| … |
(1)请补全函数图象;
(2)方程![]() x3﹣2x=﹣2实数根的个数为 ;
x3﹣2x=﹣2实数根的个数为 ;
(3)观察图象,写出该函数的两条性质.
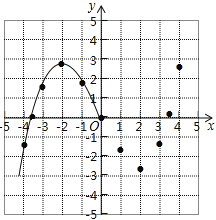
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com