
【题目】如图,抛物线y=mx2﹣2mx﹣3m(m>0)与x轴交于A、B两点,与y轴交于点C,点M为抛物线的顶点,且OC=OB.
(1)求抛物线的解析式.
(2)若抛物线上有一点P,连PC交线段BM于Q点,且S△BPQ=S△CMQ,求P点的坐标.
(3)把抛物线沿x轴正半轴平移n个单位,使平移后的抛物线交直线BC于E、F两点,且E、F关于点B对称,求n的值.
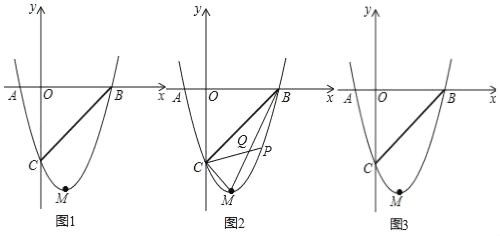
【答案】(1)y=x2﹣2x﹣3;(2)点P的坐标为(2,﹣3);(3)n=![]() .
.
【解析】
(1)先求出点A、B的坐标、OB、OC的长,从而得到点C的坐标,然后把点C的坐标代入抛物线的解析式就可解决问题;
(2)运用待定系数法可求得直线BC的解析式为y=x-3,由S△BPQ=S△CMQ可得S△PBC=S△MBC,从而可得MP∥BC,故直线MP的解析式可设为y=x+n,然后只需求出抛物线y=x2-2x-3的顶点M的坐标,就可得到直线MP的解析式为y=x-5,最后求得直线MP与抛物线的交点坐标即可;
(3)设平移后抛物线的解析式:y=(x-1-n)2-4,将y=x-3代入y=(x-1-n)2-4得:x-3=(x-1-n)2-4,从而可得到xE+xF=2n+3,依据依据点E与点F关于B对称可得到2n+3=6,从而可求得n的值.
(1)令y=0,得:mx2﹣2mx﹣3m=0,
∵m>0,
∴x2﹣2x﹣3=0,
解得:x1=﹣1,x2=3,
∴A(﹣1,0)、,B(3,0)、OB=3.
∵OC=OB=3,点C在y轴的负半轴上,
∴C(0,﹣3),
∴﹣3m=﹣3,
∴m=1,
∴抛物线的解析式为y=x2﹣2x﹣3.
(2)设直线BC的解析式为y=kx+b,则有![]() ,
,
解得:![]() ,
,
∴直线BC的解析式为y=x﹣3.
∵S△BPQ=S△CMQ,
∴S△BPQ+S△BCQ=S△CMQ+S△BCQ,
∴S△PBC=S△MBC,
∴MP∥BC,
∴直线MP的解析式可设为y=x+n.
∵抛物线y=x2﹣2x﹣3=(x﹣1)2﹣4的顶点M的坐标为(1,﹣4),
∴1+n=﹣4,
∴n=﹣5,
∴直线MP的解析式为y=x﹣5.
联立![]() ,解得:
,解得:![]() (舍去),或
(舍去),或![]() ,
,
∴点P的坐标为(2,﹣3).
(3)平移后抛物线的解析式:y=(x﹣1﹣n)2﹣4.
将y=x﹣3代入y=(x﹣1﹣n)2﹣4得:x﹣3=(x﹣1﹣n)2﹣4,整理得:x2﹣(2n+3)x+(n+1)2﹣1=0,
∴xE+xF=2n+3.
又∵点E与点F关于点B对称,
∴xE+xF=2×3,即2n+3=6,解得:n=![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】若关于x的方程x2+2(m﹣1)x+m2﹣2m﹣3=0(m为实数).
(1)求证:不论m为何值,该方程均有两个不等的实根;
(2)解方程求出两个根x1,x2(x1>x2),并求w=x1(x1+x2)+x12的最值.
查看答案和解析>>
科目:初中数学 来源: 题型:
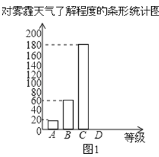
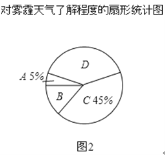
【题目】今年以来,我国持续大面积的雾霾天气让环保和健康问题成为焦点.为了调查学生对雾霾天气知识的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的三种统计图表.
对雾霾了解程度的统计表:
对雾霾的了解程度 | 百分比 |
A.非常了解 | 5% |
B.比较了解 | m |
C.基本了解 | 45% |
D.不了解 | n |
请结合统计图表,回答下列问题.
(1)本次参与调查的学生共有 人,m= ,n= ;
(2)图2所示的扇形统计图中D部分扇形所对应的圆心角是 度;
(3)请补全条形统计图;
(4)根据调查结果,学校准备开展关于雾霾知识竞赛,某班要从“非常了解”态度的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球.若摸出的两个球上的数字和为奇数,则小明去;否则小刚去.请用树状图或列表法说明这个游戏规则是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,且
,且![]() ,延长
,延长![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() ,连接
,连接![]() .下列结论中:①
.下列结论中:①![]() ;②
;②![]() 是等边角形:③
是等边角形:③![]() ;④
;④![]() ;⑤
;⑤![]() .其中正确的是( )
.其中正确的是( )
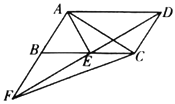
A.②③⑤B.①④⑤C.①②③D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)将△A1B1C1沿x轴方向向左平移4个单位得到△A2B2C2,画出△A2B2C2并写出顶点A2,B2,C2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 与
与![]() 均为等腰直角三角形,
均为等腰直角三角形,![]()
(1)如图1,点![]() 在
在![]() 上,点
上,点![]() 与
与![]() 重合,
重合,![]() 为线段
为线段![]() 的中点,则线段
的中点,则线段![]() 与
与![]() 的数量关系是 ,
的数量关系是 ,![]() 与
与![]() 的位置是 .
的位置是 .
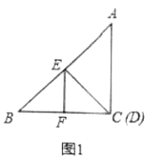
(2)如图2,在图1的基础上,将![]() 绕点
绕点![]() 顺时针旋转到如图2的位置,其中
顺时针旋转到如图2的位置,其中![]() 在一条直线上,
在一条直线上,![]() 为线段
为线段![]() 的中点,则线段
的中点,则线段![]() 与
与![]() 是否存在某种确定的数量关系和位置关系?证明你的结论.
是否存在某种确定的数量关系和位置关系?证明你的结论.
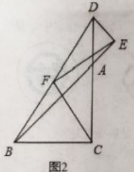
(3)若![]() 绕
绕![]() 点旋转任意一个角度到如图3的位置,
点旋转任意一个角度到如图3的位置,![]() 为线段
为线段![]() 的中点,连接
的中点,连接![]() 、
、![]() ,请你完成图3,猜想线段
,请你完成图3,猜想线段![]() 与
与![]() 的关系,并证明你的结论.
的关系,并证明你的结论.
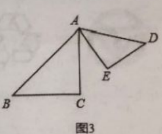
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,AB=AC=10,线段BC在轴上,BC=12,点B的坐标为(﹣3,0),线段AB交y轴于点E,过A作AD⊥BC于D,动点P从原点出发,以每秒3个单位的速度沿x轴向右运动,设运动的时间为t秒.

(1)点E的坐标为( , );
(2)当△BPE是等腰三角形时,求t的值;
(3)若点P运动的同时,△ABC以B为位似中心向右放大,且点C向右运动的速度为每秒2个单位,△ABC放大的同时高AD也随之放大,当以EP为直径的圆与动线段AD所在直线相切,求t的值和此时C点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DF、FG相交于点H.
(1)判断线段DE、FG的位置关系,并说明理由;
(2)连结CG,求证:四边形CBEG是正方形.
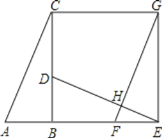
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com