
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�AB=AC=10���߶�BC�����ϣ�BC=12����B������Ϊ����3��0�����߶�AB��y���ڵ�E����A��AD��BC��D������P��ԭ���������ÿ��3����λ���ٶ���x�������˶������˶���ʱ��Ϊt�룮

��1����E���������� ������ ������
��2������BPE�ǵ���������ʱ����t��ֵ��
��3������P�˶���ͬʱ����ABC��BΪλ���������ҷŴ��ҵ�C�����˶����ٶ�Ϊÿ��2����λ����ABC�Ŵ��ͬʱ��ADҲ��֮�Ŵ���EPΪֱ����Բ�붯�߶�AD����ֱ�����У���t��ֵ�ʹ�ʱC������꣮
���𰸡���1��E��0�� 4������2��t=![]() ��t=1��t=
��t=1��t=![]() ����3����t=1, C��11��0��
����3����t=1, C��11��0��
��������
(1) �������ֱ��AB�Ľ���ʽ, ���ɵó�����;
(2) �����BE=5, �����ֱ����âٵ�BE=BPʱ,�ڵ�EB=EPʱ,�۵�PB=PEʱ, �ó���ֵ��
��;
(3) ���ȵó���PGF�ס�POE, �����ù��ɶ�����![]() , �������t��ֵ�Լ�C������.
, �������t��ֵ�Լ�C������.
�⣺��1����AB=AC��AD��BC��
��BD=CD=6��
��AB=10��
��AD=8��
��A��3��8����
��ֱ��AB�Ľ���ʽΪ��y=kx+b����![]() ��
��
��ã�![]() ��
��
��ֱ��AB�Ľ���ʽΪ��y=![]() x+4��
x+4��
��E��0��4����
�ʴ�Ϊ��0��4��
��2����B����3��0����E��0��4��
��BE=5��
����BPE�ǵ��������������������
�ٵ�BE=BPʱ��3+3t=5����ã�t=![]() ��
��
�ڵ�EB=EPʱ��3t=3����ã�t=1��
�۵�PB=PEʱ��
��PB=PE��AB=AC����ABC=��PBE��
���PEB=��ACB=��ABC��
���PBE�ס�ABC��
��![]() =
=![]() ��
��
��![]() =
=![]() ����ã�t=
����ã�t=![]() ��
��
���ϣ�t=![]() ��t=1��t=
��t=1��t=![]() ��
��
��3��������ã�C��9+2t��0����
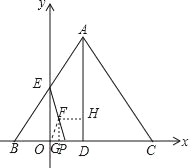
��BC=12+2t��BD=CD=6+t��OD=3+t��
��FΪEP���е㣬����OF����FH��AD��FG��OP��
��FG��EO��
���PGF�ס�POE��
��PG=OG=![]() t��FG=
t��FG=![]() EO=2��
EO=2��
��F��![]() t��2����
t��2����
��FH=GD=OD��OG=3+t��![]() t=3��
t=3��![]() t��
t��
�ߡ�F�붯�߶�AD����ֱ�����У�FH=![]() EP=3��
EP=3��![]() t��
t��
��Rt��EOP��EP2=OP2+EO2
��4��3��![]() t��2=��3t��2+16
t��2=��3t��2+16
��ã�t1=1��t2=��![]() ����ȥ����
����ȥ����
�൱t=1ʱ����F�붯�߶�AD����ֱ�����У���ʱC��11��0����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ��ƽ��ֱ������ϵ����
��ƽ��ֱ������ϵ����![]() �ύ�ڵ�A����B����3��3��Ҳ��ֱ��
�ύ�ڵ�A����B����3��3��Ҳ��ֱ��![]() �ϣ�����B������ƽ��1����λ���ȣ�������ƽ��2����λ���ȵõ���C����CҲ��ֱ��
�ϣ�����B������ƽ��1����λ���ȣ�������ƽ��2����λ���ȵõ���C����CҲ��ֱ��![]() ��.
��.
��1�����C�������ֱ��![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����ֱ֪��![]() ��
��![]() ������B����
������B����![]() �ύ�ڵ�E�����ABE�����.
�ύ�ڵ�E�����ABE�����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=mx2��2mx��3m��m��0����x�ύ��A��B���㣬��y�ύ�ڵ�C����MΪ�����ߵĶ��㣬��OC=OB��
��1���������ߵĽ���ʽ��
��2��������������һ��P����PC���߶�BM��Q�㣬��S��BPQ=S��CMQ����P������꣮
��3������������x��������ƽ��n����λ��ʹƽ�ƺ�������߽�ֱ��BC��E��F���㣬��E��F���ڵ�B�Գƣ���n��ֵ��
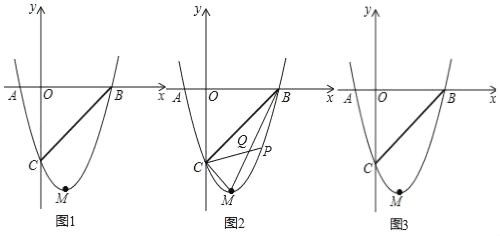
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʵ��a��b�����ǿ�����min{a��b}��ʾa��b�����н�С����������min{3����1}����1��min{2��2}��2. ���Ƶأ�������y1��y2����x�ĺ�������y��min{y1�� y2}��ʾ����y1��y2����ȡС��������
��1����y1��x��y2��![]() ������y��min{x��
������y��min{x�� ![]() }��ͼ��Ӧ���� �е�ʵ�߲��֣�
}��ͼ��Ӧ���� �е�ʵ�߲��֣�

��2��������ͼ������ʵ���������y��min{(x��2)2�� (x��2)2}��ͼ��д����ͼ���������ͬ���ʣ�

�� ��
�� ��
�� ��
��3������y��min{(x��4)2�� (x��2)2}��ͼ����� �Գƣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ֱ��ԡ�ABC�ı�AB��AC�����������ȱ������Ρ�ABD����ACE������BE��CD����F������AF��
��1����֤����ACD�ա�AEB��
��2����֤��AF+BF+CF=CD��
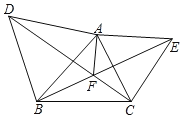
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ͬʱ������A�س�������һ����ֱ�Ĺ�·����ǰ�����400ǧ��B�أ�1Сʱ��������Ʒ����A�أ�����������ԭ�ٷ���A��ȡ��Ʒ��ȡ����Ʒ����������25%��������B�أ����е�ͷ��ȡ��Ʒ��ʱ����Բ��ƣ����������˼�ľ���yǧ���������ʻ��ʱ��xСʱ֮��IJ��ֺ���ͼ����ͼ��ʾ��������B��ʱ������B�صľ�����_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧϰС�����о�����y=![]() x3��2x��ͼ��������ʱ�����б�����㲢������ͼ���һ���֣�
x3��2x��ͼ��������ʱ�����б�����㲢������ͼ���һ���֣�
x | �� | ��4 | ��3.5 | ��3 | ��2 | ��1 | 0 | 1 | 2 | 3 | 3.5 | 4 | �� |
y | �� | �� | �� |
|
|
| 0 | �� | �� | �� |
|
| �� |
��1���벹ȫ����ͼ��
��2������![]() x3��2x=��2ʵ�����ĸ���Ϊ�� ����
x3��2x=��2ʵ�����ĸ���Ϊ�� ����
��3���۲�ͼ��д���ú������������ʣ�
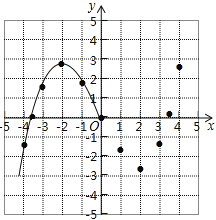
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һֻ�����IJ�����װ�к��� 3 �������� 1 ������Щ�����ɫ�ⶼ��ͬ������ҡ�ȣ�
(1)�Ӳ�����һ������ 1 ����������������ǡ�ǻ������ĸ��ʣ�
(2)�Ӳ�����һ������ 2 ����������������ǡ��һ��һ�����ĸ���(���� ����״ͼ�������б����ķ���д���������)��
�鿴�𰸺ͽ���>>
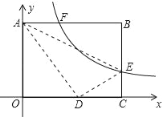
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCO����ƽ��ֱ������ϵ�У����ж���B������Ϊ��5��3����E��BC����һ�㣬����ABE��AE���ۣ���B�պ���OC���ϵĵ�D�غϣ�����E�ķ���������y=![]() ��ͼ�����AB���ڵ�F�����߶�AF�ij�Ϊ_____��
��ͼ�����AB���ڵ�F�����߶�AF�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com