
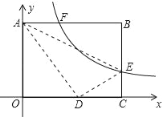
【题目】如图,将矩形ABCO放在平面直角坐标系中,其中顶点B的坐标为(5,3),E是BC边上一点,将△ABE沿AE翻折,点B刚好与OC边上的点D重合,过点E的反比例函数y=![]() 的图象与边AB交于点F,则线段AF的长为_____.
的图象与边AB交于点F,则线段AF的长为_____.
【答案】![]()
【解析】
根据△ABE与△ADE是全等可得BE=DE,设BE=a=DE, CE=3-a,在Rt△AOD中,AD=AB=5,AO=3,由勾股定理![]() ,可得a的值,可求出反比例函数的表达式,可求出AF的长.
,可得a的值,可求出反比例函数的表达式,可求出AF的长.
解:根据题目条件可知, △ABE与△ADE是全等的,所以BE=DE,
设BE=a=DE, CE=3-a,
在Rt△AOD中,AD=AB=5,AO=3,由勾股定理![]() ,
,
即OD=![]() =4,
=4,
所以DC=OC-OD=1,
在Rt△DCE中, 由勾股定理![]() ,
,
即![]() ,求出a=
,求出a=![]() ,CE=
,CE=![]() ,
,
所以E(5,![]() ),
),
因为点E在反比例反函数上, 可得k =5![]()
![]() =
=![]() ,即可y=
,即可y=![]() ,
,
又因为点F在反比例函数上, 设F(b,3),
可得:b=![]() =
=![]() ,即AF的长为
,即AF的长为![]() .
.
故答案:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,AB=AC=10,线段BC在轴上,BC=12,点B的坐标为(﹣3,0),线段AB交y轴于点E,过A作AD⊥BC于D,动点P从原点出发,以每秒3个单位的速度沿x轴向右运动,设运动的时间为t秒.

(1)点E的坐标为( , );
(2)当△BPE是等腰三角形时,求t的值;
(3)若点P运动的同时,△ABC以B为位似中心向右放大,且点C向右运动的速度为每秒2个单位,△ABC放大的同时高AD也随之放大,当以EP为直径的圆与动线段AD所在直线相切,求t的值和此时C点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
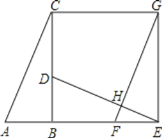
【题目】如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DF、FG相交于点H.
(1)判断线段DE、FG的位置关系,并说明理由;
(2)连结CG,求证:四边形CBEG是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
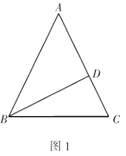
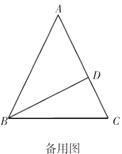
如图1,![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,
,![]() 且
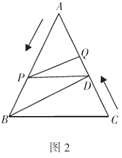
且![]() ;如图2,在图1的基础上,动点
;如图2,在图1的基础上,动点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 的速度沿线段
的速度沿线段![]() 向点
向点![]() 运动,同时动点
运动,同时动点![]() 从点
从点![]() 出发以相同速度沿线段
出发以相同速度沿线段![]() 向点
向点![]() 运动,当其中一点到达终点时另外一点也随之停止运动,设点
运动,当其中一点到达终点时另外一点也随之停止运动,设点![]() 运动的时间为
运动的时间为![]() 秒.
秒.
(1)求![]() 的长;
的长;
(2)当![]() 的其中一边与
的其中一边与![]() 平行时(
平行时(![]() 与
与![]() 不重合),求
不重合),求![]() 的值;
的值;
(3)点![]() 在线段
在线段![]() 上运动的过程中,是否存在以
上运动的过程中,是否存在以![]() 为腰的
为腰的![]() 是等腰三角形?若存在,求出
是等腰三角形?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每到春夏交替时节,雌性杨树会以满天飞絮的方式来传播下一代,漫天飞舞的杨絮易引发皮肤病、呼吸道疾病等,给人们造成困扰,为了解市民对治理杨絮方法的赞同情况,某课题小组随机调查了部分市民(问卷调查表如表所示),并根据调查结果绘制了如下尚不完整的统计图.
治理杨絮一一您选哪一项?(单选)
A.减少杨树新增面积,控制杨树每年的栽种量
B.调整树种结构,逐渐更换现有杨树
C.选育无絮杨品种,并推广种植
D.对雌性杨树注射生物干扰素,避免产生飞絮
E.其他
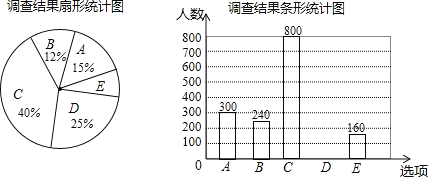
根据以上统计图,解答下列问题:
(1)本次接受调查的市民共有 人;
(2)扇形统计图中,扇形E的圆心角度数是 ;
(3)请补全条形统计图;
(4)若该市约有90万人,请估计赞同“选育无絮杨品种,并推广种植”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宜兴在“创建文明城市”行动中,某社区计划对面积为2160m2的区域进行绿化.经投标,由甲、乙两个工程队来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为480m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积;
(2)设甲工程队施工x天,乙工程队施工y天,刚好完成绿化任务,求y与x的函数表达式;
(3)若甲队每天绿化费用是0.8万元,乙队每天绿化费用为0.35万元,且甲、乙两队施工的总天数不超过26天,则如何安排甲乙两队施工的天数,使施工总费用最低?并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是圆O的直径,C、D是圆O上的点,且OC∥BD,AD分别与BC、OC相交于点E、F.则下列结论:
①AD⊥BD;②∠AOC=∠ABC;③CB平分∠ABD;④AF=DF;⑤BD=2OF.
其中一定成立的是( )

A.①③⑤ B.②③④ C.②④⑤ D.①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
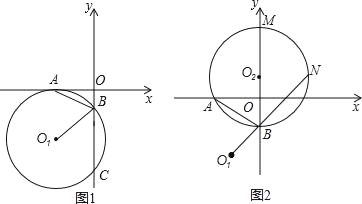
【题目】如图1在平面直角坐标系中,⊙O1与x轴切于A(﹣3,0)与y轴交于B、C两点,BC=8,连AB.
(1)求证:∠ABO1=∠ABO;
(2)求AB的长;
(3)如图2,过A、B两点作⊙O2与y轴的正半轴交于M,与O1B的延长线交于N,当⊙O2的大小变化时,得出下列两个结论:①BM﹣BN的值不变;②BM+BN的值不变.其中有且只有一个结论正确,请判断正确结论并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形![]() ,
,![]() ,
,![]() 与
与![]() 互补,以点
互补,以点![]() 为顶点作一个角,角的两边分别交线段
为顶点作一个角,角的两边分别交线段![]() ,
,![]() 于点
于点![]() ,
,![]() ,且
,且![]() ,连接
,连接![]() ,试探究:线段
,试探究:线段![]() ,
,![]() ,
,![]() 之间的数量关系.
之间的数量关系.
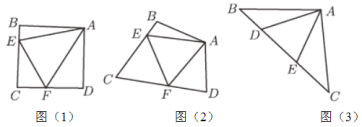
(1)如图(1),当![]() 时,
时,![]() ,
,![]() ,
,![]() 之间的数量关系为___________.
之间的数量关系为___________.
(2)在图(2)的条件下(即不存在![]() ),线段
),线段![]() ,
,![]() ,
,![]() 之间的数量关系是否仍然成立?若成立,请完成证明;若不成立,请说明理由.
之间的数量关系是否仍然成立?若成立,请完成证明;若不成立,请说明理由.
(3)如图(3),在腰长为![]() 的等腰直角三角形
的等腰直角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() 均在边
均在边![]() 上,且
上,且![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com