
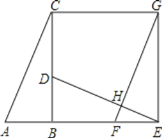
【题目】如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DF、FG相交于点H.
(1)判断线段DE、FG的位置关系,并说明理由;
(2)连结CG,求证:四边形CBEG是正方形.
【答案】(1)FG⊥ED,理由详见解析;(2)详见解析
【解析】
(1)由旋转及平移的性质可得到∠DEB+∠GFE=90°,可得出结论;
(2)由旋转和平移的性质可得BE=CB,CG∥BE,从而可证明四边形CBEG是矩形,再结合CB=BE可证明四边形CBEG是正方形.
(1)FG⊥ED.
理由如下:
∵△ABC绕点B顺时针旋转90°至△DBE后,
∴∠DEB=∠ACB,
∵把△ABC沿射线平移至△FEG,
∴∠GFE=∠A,
∵∠ABC=90°,
∴∠A+∠ACB=90°,
∴∠DEB+∠GFE=90°,
∴∠FHE=90°,
∴FG⊥ED;
(2)根据旋转和平移可得∠GEF=90°,∠CBE=90°,CG∥EB,CB=BE,
∵CG∥EB,
∴∠BCG=∠CBE=90°,
∴∠BCG=90°,
∴四边形BCGE是矩形,
∵CB=BE,
∴四边形CBEG是正方形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
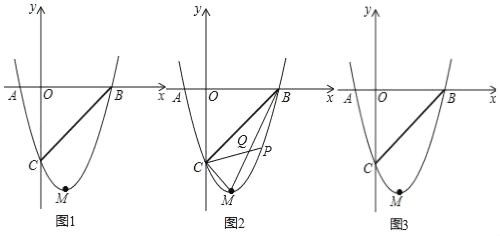
【题目】如图,抛物线y=mx2﹣2mx﹣3m(m>0)与x轴交于A、B两点,与y轴交于点C,点M为抛物线的顶点,且OC=OB.
(1)求抛物线的解析式.
(2)若抛物线上有一点P,连PC交线段BM于Q点,且S△BPQ=S△CMQ,求P点的坐标.
(3)把抛物线沿x轴正半轴平移n个单位,使平移后的抛物线交直线BC于E、F两点,且E、F关于点B对称,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
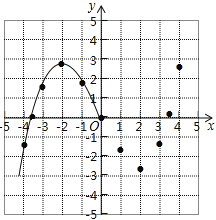
【题目】某学习小组在研究函数y=![]() x3﹣2x的图象与性质时,已列表、描点并画出了图象的一部分.
x3﹣2x的图象与性质时,已列表、描点并画出了图象的一部分.
x | … | ﹣4 | ﹣3.5 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 3.5 | 4 | … |
y | … | ﹣ | ﹣ |
|
|
| 0 | ﹣ | ﹣ | ﹣ |
|
| … |
(1)请补全函数图象;
(2)方程![]() x3﹣2x=﹣2实数根的个数为 ;
x3﹣2x=﹣2实数根的个数为 ;
(3)观察图象,写出该函数的两条性质.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一只不透明的布袋中装有红球 3 个、黄球 1 个,这些球除颜色外都相同,均匀摇匀.
(1)从布袋中一次摸出 1 个球,计算“摸出的球恰是黄球”的概率;
(2)从布袋中一次摸出 2 个球,计算“摸出的球恰是一红一黄”的概率(用“ 画树状图”或“列表”的方法写出计算过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
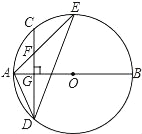
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足![]() ,连接AF并延长交⊙O于点E,连接AD,DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED; ②FG=2;③tan∠E=
,连接AF并延长交⊙O于点E,连接AD,DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED; ②FG=2;③tan∠E=![]() ; ④S△DEF=4
; ④S△DEF=4![]() ,其中正确的是( )
,其中正确的是( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
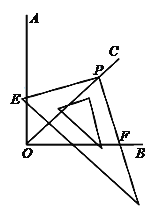
【题目】如图,∠AOB=90°,将三角尺的直角顶点P落在∠AOB的平分线OC的任意一点上,使三角尺的两条直角边与∠AOB的两边分别相交于点E、F。证明:PE=PF。
查看答案和解析>>
科目:初中数学 来源: 题型:
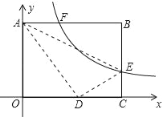
【题目】如图,将矩形ABCO放在平面直角坐标系中,其中顶点B的坐标为(5,3),E是BC边上一点,将△ABE沿AE翻折,点B刚好与OC边上的点D重合,过点E的反比例函数y=![]() 的图象与边AB交于点F,则线段AF的长为_____.
的图象与边AB交于点F,则线段AF的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角三角形ABC中,直线l为BC的中垂线,射线m为∠ABC的角平分线,直线l与m相交于点P.若∠BAC=60°,∠ACP=24°,则∠ABP的度数是( )

A. 24° B. 30° C. 32° D. 36°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com