
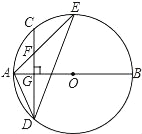
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足![]() ,连接AF并延长交⊙O于点E,连接AD,DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED; ②FG=2;③tan∠E=
,连接AF并延长交⊙O于点E,连接AD,DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED; ②FG=2;③tan∠E=![]() ; ④S△DEF=4
; ④S△DEF=4![]() ,其中正确的是( )
,其中正确的是( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
【答案】B
【解析】
由垂径定理得出CG=DG,![]() ,得出圆周角∠ADF=∠E,再由公共角相等,即可得出△ADF∽△AED,①正确;
,得出圆周角∠ADF=∠E,再由公共角相等,即可得出△ADF∽△AED,①正确;
由已知条件求出FD,得出CD、CG,即可求出FG=2,②正确;
由相交弦定理求出EF,得出AE,由△ADF∽△AED,得出对应边成比例![]() ,求出AD2=21,由勾股定理求出AG,得出tan∠E=tan∠ADF=
,求出AD2=21,由勾股定理求出AG,得出tan∠E=tan∠ADF=![]() ,③错误;
,③错误;
作EM⊥CD于M,则EM∥AB,证出△EFM∽△AFG,得出比例式![]() ,求出ME,即可得出S△DEF=
,求出ME,即可得出S△DEF=![]() FDME=4
FDME=4![]() ,④正确.
,④正确.
∵AB是⊙O的直径,弦CD⊥AB,
∴CG=DG,![]() ,∠AGF=∠AGD=90°,
,∠AGF=∠AGD=90°,
∴∠ADF=∠E,
又∵∠DAF=∠EAD,
∴△ADF∽△AED,
∴①正确;
∵![]() ,CF=2,
,CF=2,
∴FD=6,
∴CD=8,
∵CG=DG,
∴CG=DG=4,
∴FG=2,
∴②正确;
∵AFEF=CFFD,
即3EF=2×6,
∴EF=4,
∴AE=7,
∵△ADF∽△AED,
∴![]() ,
,
∴AD2=AE×AF=7×3=21,
在Rt△ADG中,AG=![]() ,
,
∴tan∠E=tan∠ADF=![]() ,
,
∴③错误;
作EM⊥CD于M,如图所示:
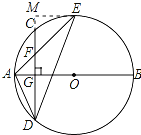
则EM∥AB,
∴△EFM∽△AFG,
∴![]() ,
,![]()
∴ME=![]() ,
,
∴S△DEF=![]() FDME=
FDME=![]() ×6×
×6×![]() =4
=4![]() ,
,
∴④正确;
故选B.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)将△A1B1C1沿x轴方向向左平移4个单位得到△A2B2C2,画出△A2B2C2并写出顶点A2,B2,C2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
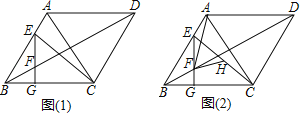
【题目】如图,在菱形ABCD中,∠BAD=120°,E为AB边上一点,过E作EG⊥BC于点G,交对角线BD于点F.
(1)如图(1),若∠ACE=15°,BC=6,求EF的长;
(2)如图(2),H为CE的中点,连接AF,FH,求证:AF=2FH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题解决:如图,在四边形ABCD中,∠BAD=α,∠BCD=180°﹣α,BD平分∠ABC.
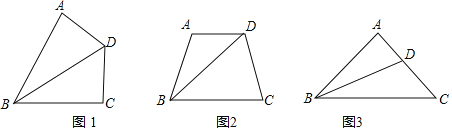
①如图1,若α=90°,根据教材中一个重要性质直接可得AD=CD,这个性质是 ;
②在图2中,求证:AD=CD;
(2)拓展探究:根据(1)的解题经验,请解决如下问题:如图3,在等腰△ABC中,∠BAC=100°,BD平分∠ABC,求证BD+AD=BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为1的小正方形网格中,△AOB的顶点均在格点上.
(1)B点关于y轴的对称点坐标为 ;
(2)将△AOB向左平移3个单位长度得到△A1O1B1,请画出△A1O1B1;
(3)在(2)的条件下,A1的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
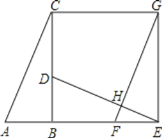
【题目】如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DF、FG相交于点H.
(1)判断线段DE、FG的位置关系,并说明理由;
(2)连结CG,求证:四边形CBEG是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每到春夏交替时节,雌性杨树会以满天飞絮的方式来传播下一代,漫天飞舞的杨絮易引发皮肤病、呼吸道疾病等,给人们造成困扰,为了解市民对治理杨絮方法的赞同情况,某课题小组随机调查了部分市民(问卷调查表如表所示),并根据调查结果绘制了如下尚不完整的统计图.
治理杨絮一一您选哪一项?(单选)
A.减少杨树新增面积,控制杨树每年的栽种量
B.调整树种结构,逐渐更换现有杨树
C.选育无絮杨品种,并推广种植
D.对雌性杨树注射生物干扰素,避免产生飞絮
E.其他
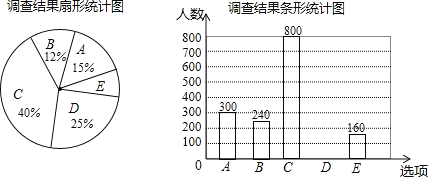
根据以上统计图,解答下列问题:
(1)本次接受调查的市民共有 人;
(2)扇形统计图中,扇形E的圆心角度数是 ;
(3)请补全条形统计图;
(4)若该市约有90万人,请估计赞同“选育无絮杨品种,并推广种植”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
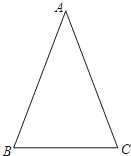
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=![]() .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述对角的正对定义,解下列问题:
(1)求sad60°的值;
(2)对于0°<A<180°,求∠A的正对值sadA的取值范围.
(3)已知sinα=![]() ,其中α为锐角,试求sadα的值.
,其中α为锐角,试求sadα的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com