
【题目】(1)问题解决:如图,在四边形ABCD中,∠BAD=α,∠BCD=180°﹣α,BD平分∠ABC.
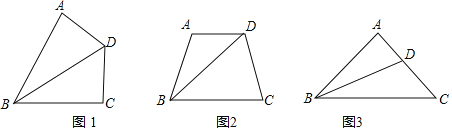
①如图1,若α=90°,根据教材中一个重要性质直接可得AD=CD,这个性质是 ;
②在图2中,求证:AD=CD;
(2)拓展探究:根据(1)的解题经验,请解决如下问题:如图3,在等腰△ABC中,∠BAC=100°,BD平分∠ABC,求证BD+AD=BC.
【答案】(1)①角平分线上的点到角的两边距离相等;②见解析;(2)见解析.
【解析】
(1)①根据角平分线的性质定理即可解决问题;
②如图2中,作DE⊥BA于E,DF⊥BC于F.只要证明△DEA≌△DFC即可解决问题;
(2)如图3中,在BC时截取BK=BD,BT=BA,连接DK.首先证明DK=CK,再证明△DBA≌△DBT,推出AD=DT,∠A=∠BTD=100°,推出∠DTK=∠DKT=80°,推出DT=DK=CK,由此即可解决问题;
(1)①根据角平分线的性质定理可知AD=CD.
所以这个性质是角平分线上的点到角的两边距离相等.
故答案为:角平分线上的点到角的两边距离相等.
②如图2中,作DE⊥BA于E,DF⊥BC于F.
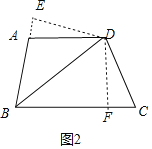
∵BD平分∠EBF,DE⊥BE,DF⊥BF,
∴DE=DF,
∵∠BAD+∠C=180°,∠BAD+∠EAD=180°,
∴∠EAD=∠C,
∵∠E=∠DFC=90°,
∴△DEA≌△DFC,
∴DA=DC.
(2)如图3中,在BC上截取BK=BD,BT=BA,连接DK.
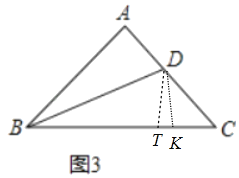
∵AB=AC,∠A=100°,
∴∠ABC=∠C=40°,
∵BD平分∠ABC,
∴∠DBK=![]() ∠ABC=20°,
∠ABC=20°,
∵BD=BK,
∴∠BKD=∠BDK=80°,
∵∠BKD=∠C+∠KDC,
∴∠KDC=∠C=40°,
∴DK=CK,
∵BD=BD,BA=BT,∠DBA=∠DBT,
∴△DBA≌△DBT,
∴AD=DT,∠A=∠BTD=100°,
∴∠DTK=∠DKT=80°,
∴DT=DK=CK,
∴BD+AD=BK+CK=BC.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,已知AB=AC,∠BAC=90°,E为边AC上一点,连接BE.
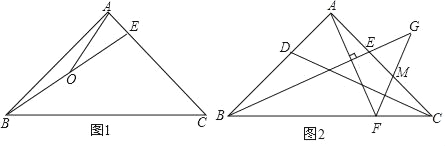
(1)如图1,若∠ABE=15°,O为BE中点,连接AO,且AO=1,求BC的长;
(2)如图2,D为AB上一点,且满足AE=AD,过点A作AF⊥BE交BC于点F,过点F作FG⊥CD交BE的延长线于点G,交AC于点M,求证:BG=AF+FG.
查看答案和解析>>
科目:初中数学 来源: 题型:
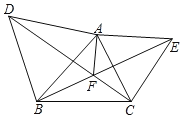
【题目】如图,分别以△ABC的边AB,AC向外作两个等边三角形△ABD,△ACE.连接BE、CD交点F,连接AF.
(1)求证:△ACD≌△AEB;
(2)求证:AF+BF+CF=CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
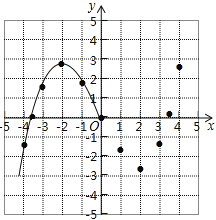
【题目】某学习小组在研究函数y=![]() x3﹣2x的图象与性质时,已列表、描点并画出了图象的一部分.
x3﹣2x的图象与性质时,已列表、描点并画出了图象的一部分.
x | … | ﹣4 | ﹣3.5 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 3.5 | 4 | … |
y | … | ﹣ | ﹣ |
|
|
| 0 | ﹣ | ﹣ | ﹣ |
|
| … |
(1)请补全函数图象;
(2)方程![]() x3﹣2x=﹣2实数根的个数为 ;
x3﹣2x=﹣2实数根的个数为 ;
(3)观察图象,写出该函数的两条性质.
查看答案和解析>>
科目:初中数学 来源: 题型:
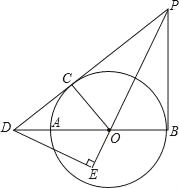
【题目】如图,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接PB,∠EDB=∠EPB.
(1)求证:PB是⊙O的切线.
(2)若PB=3,DB=4,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一只不透明的布袋中装有红球 3 个、黄球 1 个,这些球除颜色外都相同,均匀摇匀.
(1)从布袋中一次摸出 1 个球,计算“摸出的球恰是黄球”的概率;
(2)从布袋中一次摸出 2 个球,计算“摸出的球恰是一红一黄”的概率(用“ 画树状图”或“列表”的方法写出计算过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
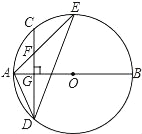
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足![]() ,连接AF并延长交⊙O于点E,连接AD,DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED; ②FG=2;③tan∠E=
,连接AF并延长交⊙O于点E,连接AD,DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED; ②FG=2;③tan∠E=![]() ; ④S△DEF=4
; ④S△DEF=4![]() ,其中正确的是( )
,其中正确的是( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
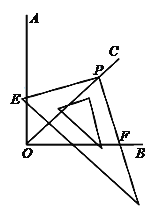
【题目】如图,∠AOB=90°,将三角尺的直角顶点P落在∠AOB的平分线OC的任意一点上,使三角尺的两条直角边与∠AOB的两边分别相交于点E、F。证明:PE=PF。
查看答案和解析>>
科目:初中数学 来源: 题型:
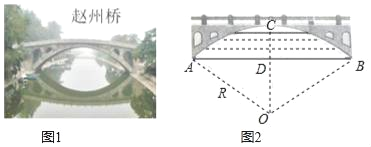
【题目】赵州桥是我国建筑史上的一大创举,它距今约1400年,历经无数次洪水冲击和8次地震却安然无恙.如图,若桥跨度AB约为40米,主拱高CD约10米,
(1)如图1,尺规作图,找到桥弧所在圆的圆心O(保留作图痕迹);
(2)如图2,求桥弧AB所在圆的半径R.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com