
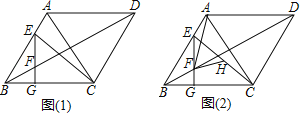
【题目】如图,在菱形ABCD中,∠BAD=120°,E为AB边上一点,过E作EG⊥BC于点G,交对角线BD于点F.
(1)如图(1),若∠ACE=15°,BC=6,求EF的长;
(2)如图(2),H为CE的中点,连接AF,FH,求证:AF=2FH.
【答案】(1)EF=4﹣![]() ;(2)见解析
;(2)见解析
【解析】
(1)首先证明EG=CG,设BG=x,则EG=CG=![]() x,根据BC=4,构建方程求出x,证明EF=BF,求出BF即可解决问题.
x,根据BC=4,构建方程求出x,证明EF=BF,求出BF即可解决问题.
(2)如图2,作CM⊥BC交FH的延长线于M,连接AM,AH.利用全等三角形的性质证明△FAM是等边三角形即可解决问题.
解:(1)如图1中,
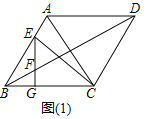
∵四边形ABCD是菱形,
∵AB=BC=CD=AD=6,AD∥BC,
∴∠ABC=180°﹣∠BAD=60°,
∴△ABC是等边三角形,
∴∠ACB=60°,
∵∠ACE=15°,
∴∠ECG=∠ACB﹣∠ACE=45°,
∵EG⊥CG,
∴∠EGC=90°,
∴EG=CG,
设BG=x,则EG=CG=![]() x,
x,
∴x+![]() x=4,
x=4,
∴x=2![]() ﹣2,
﹣2,
∵四边形ABCD是菱形,
∴∠FBG=∠EBF=30°,
∵∠BEG=30°,
∴FB=FE,
∵BF=![]() =
=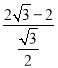 =4﹣
=4﹣![]() ,
,
∴EF=4﹣![]() .
.
(2)如图2,作CM⊥BC交FH的延长线于M,连接AM,AH.

∵EG⊥BC,MC⊥BC,
∴EF∥CM,
∴∠FEH=∠HCM,
∵∠EHF=∠CHM,EH=CH,
∴△EFH≌△CMH(ASA),
∴EF=CM,FH=HM,
∵EF=BF,
∴BF=CM,
∵∠ABF=∠ACM=30°,BA=CA,
∴△BAF≌△CAM(SAS),
∴AF=AM,∠BAF=∠CAM,
∴∠FAM=∠BAC=60°,
∴△FAM是等边三角形,
∵FH=HM,
∴AH⊥FM,∠FAH=![]() ∠FAM=
∠FAM=![]() ×60°=30°,
×60°=30°,
∴AF=2FH.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,等腰梯形ABCD的顶点坐标分别为A(1,1),B(2,﹣1),C(﹣2,﹣1),D(﹣1,1).以A为对称中心作点P(0,2)的对称点P1,以B为对称中心作点P1的对称点P2,以C为对称中心作点P2的对称点P3,以D为对称中心作点P3的对称点P4,…,重复操作依次得到点P1,P2,…,则点P2010的坐标是( )
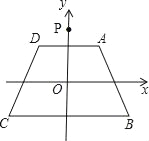
A. (2010,2) B. (2010,﹣2) C. (2012,﹣2) D. (0,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初三(1)班要从2男2女共4名同学中选人做晨会的升旗手.
(1)若从这4人中随机选1人,则所选的同学性别为男生的概率是 .
(2)若从这4人中随机选2人,求这2名同学性别相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
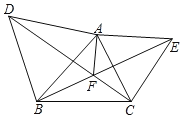
【题目】如图,分别以△ABC的边AB,AC向外作两个等边三角形△ABD,△ACE.连接BE、CD交点F,连接AF.
(1)求证:△ACD≌△AEB;
(2)求证:AF+BF+CF=CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (a≠0)的图象如图所示,
(a≠0)的图象如图所示,
有下列结论:
①a、b同号;
②当x=1和x=3时,函数值相等;
③4a+b=0;
④当-1<x<5时,y<0.
其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
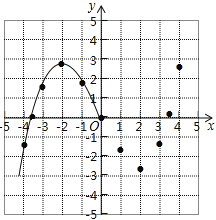
【题目】某学习小组在研究函数y=![]() x3﹣2x的图象与性质时,已列表、描点并画出了图象的一部分.
x3﹣2x的图象与性质时,已列表、描点并画出了图象的一部分.
x | … | ﹣4 | ﹣3.5 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 3.5 | 4 | … |
y | … | ﹣ | ﹣ |
|
|
| 0 | ﹣ | ﹣ | ﹣ |
|
| … |
(1)请补全函数图象;
(2)方程![]() x3﹣2x=﹣2实数根的个数为 ;
x3﹣2x=﹣2实数根的个数为 ;
(3)观察图象,写出该函数的两条性质.
查看答案和解析>>
科目:初中数学 来源: 题型:
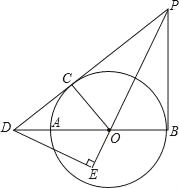
【题目】如图,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接PB,∠EDB=∠EPB.
(1)求证:PB是⊙O的切线.
(2)若PB=3,DB=4,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足![]() ,连接AF并延长交⊙O于点E,连接AD,DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED; ②FG=2;③tan∠E=
,连接AF并延长交⊙O于点E,连接AD,DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED; ②FG=2;③tan∠E=![]() ; ④S△DEF=4
; ④S△DEF=4![]() ,其中正确的是( )
,其中正确的是( )
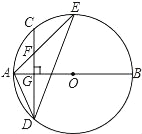
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若△ABC内一点P满足∠PAC=∠PCB=∠PBA,则称点P为△ABC的布罗卡尔点,三角形的布罗卡尔点是法国数学家和数学教育家克雷尔首次发现,后来被数学爱好者法国军官布罗卡尔重新发现,并用他的名字命名,布罗卡尔点的再次发现,引发了研究“三角形几何”的热潮.已知△ABC中,CA=CB,∠ACB=120°,P为△ABC的布罗卡尔点,若PA=![]() ,则PB+PC=_____.
,则PB+PC=_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com