
【题目】如图,锐角△ABC 中 BC=a,AC=b,AB=c,记三角形 ABC 的面积为 S.
(1)求证:S=![]() absinC;
absinC;
(2)求证:![]() .
.
【答案】(1)见解析;(2)见解析
【解析】
(1)过A作AH⊥BC于H,可得AH=b×sinC,依据三角形ABC的面积=![]() ×BC×AH,即可得到S=
×BC×AH,即可得到S=![]() absinC;
absinC;
(2)过点C作CD⊥AB于D,在Rt△ADC和Rt△BDC中,∠ADC=∠BDC=90°,可得sinA=![]() ,sinB=
,sinB=![]() ,由此可得
,由此可得![]() .同理可证
.同理可证![]() ,进而得到结论.
,进而得到结论.
(1)如图,过A作AH⊥BC于H,则
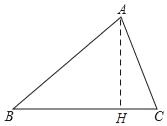
Rt△ACH中,sinC=![]() ,
,
∴AH=b×sinC,
∵三角形ABC的面积=![]() ×BC×AH,
×BC×AH,
∴S=![]() absinC;
absinC;
(2)如图,过点C作CD⊥AB于D,
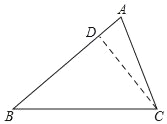
在Rt△ADC和Rt△BDC中,∠ADC=∠BDC=90°,
则sinA=![]() ,sinB=
,sinB=![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.
过点A作AH⊥BC于H,同理可证![]() .
.
∴![]() .
.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,若∠DAB的平分线AE交CD于E,连结BE,且BE也平分∠ABC,则以下的命题中正确的个数是( )
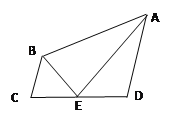
①BC+AD=AB ; ②E为CD中点
③∠AEB=90°; ④S△ABE=![]() S四边形ABCD
S四边形ABCD
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线L,过点B作一直线(在山的旁边经过),与L相交于D点,经测量∠ABD=135°,BD=800米,求直线L上距离D点多远的C处开挖?(![]() ≈1.414,精确到1米)
≈1.414,精确到1米)
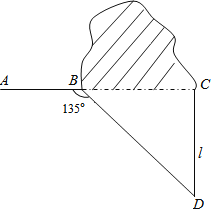
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DF、FG相交于点H.
(1)判断线段DE、FG的位置关系,并说明理由;
(2)连结CG,求证:四边形CBEG是正方形.
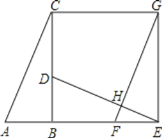
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6cm,∠ABC=30°,动点P从点B出发,在BA边上以每秒2cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒![]() cm的速度向点B匀速运动,运动时间为t秒(0≤t≤6),连接PQ,以PQ为直径作⊙O.
cm的速度向点B匀速运动,运动时间为t秒(0≤t≤6),连接PQ,以PQ为直径作⊙O.
(1)当t=1时,求△BPQ的面积;
(2)设⊙O的面积为y,求y与t的函数解析式;
(3)若⊙O与Rt△ABC的一条边相切,求t的值.
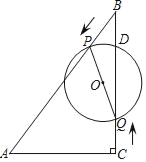
查看答案和解析>>
科目:初中数学 来源: 题型:
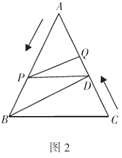
【题目】综合与实践:
如图1,![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,
,![]() 且
且![]() ;如图2,在图1的基础上,动点
;如图2,在图1的基础上,动点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 的速度沿线段
的速度沿线段![]() 向点
向点![]() 运动,同时动点
运动,同时动点![]() 从点
从点![]() 出发以相同速度沿线段
出发以相同速度沿线段![]() 向点
向点![]() 运动,当其中一点到达终点时另外一点也随之停止运动,设点
运动,当其中一点到达终点时另外一点也随之停止运动,设点![]() 运动的时间为
运动的时间为![]() 秒.
秒.
(1)求![]() 的长;
的长;
(2)当![]() 的其中一边与
的其中一边与![]() 平行时(
平行时(![]() 与
与![]() 不重合),求
不重合),求![]() 的值;
的值;
(3)点![]() 在线段
在线段![]() 上运动的过程中,是否存在以
上运动的过程中,是否存在以![]() 为腰的
为腰的![]() 是等腰三角形?若存在,求出
是等腰三角形?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
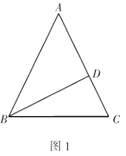
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宜兴在“创建文明城市”行动中,某社区计划对面积为2160m2的区域进行绿化.经投标,由甲、乙两个工程队来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为480m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积;
(2)设甲工程队施工x天,乙工程队施工y天,刚好完成绿化任务,求y与x的函数表达式;
(3)若甲队每天绿化费用是0.8万元,乙队每天绿化费用为0.35万元,且甲、乙两队施工的总天数不超过26天,则如何安排甲乙两队施工的天数,使施工总费用最低?并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌的饮水机接通电源后就进入自动程序:开机加热到水温 100℃, 停止加热,水温开始下降,此时水温 y(℃)与开机后用时 x(min)成反比 例关系,直至水温降至 30℃,饮水机关机.饮水机关机后即刻自动开机,重 复上述自动程序.若在水温为 30℃时,接通电源后,水温 y(℃)和时间 x(min)的关系如图所示,水温从 100℃降到 35℃所用的时间是________min.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com