
【题目】已知四边形![]() ,
,![]() ,
,![]() 与
与![]() 互补,以点
互补,以点![]() 为顶点作一个角,角的两边分别交线段
为顶点作一个角,角的两边分别交线段![]() ,
,![]() 于点
于点![]() ,
,![]() ,且
,且![]() ,连接
,连接![]() ,试探究:线段
,试探究:线段![]() ,
,![]() ,
,![]() 之间的数量关系.
之间的数量关系.
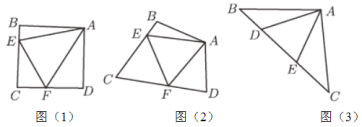
(1)如图(1),当![]() 时,
时,![]() ,
,![]() ,
,![]() 之间的数量关系为___________.
之间的数量关系为___________.
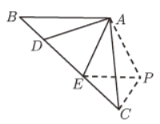
(2)在图(2)的条件下(即不存在![]() ),线段
),线段![]() ,
,![]() ,
,![]() 之间的数量关系是否仍然成立?若成立,请完成证明;若不成立,请说明理由.
之间的数量关系是否仍然成立?若成立,请完成证明;若不成立,请说明理由.
(3)如图(3),在腰长为![]() 的等腰直角三角形
的等腰直角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() 均在边
均在边![]() 上,且
上,且![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
【答案】(1)![]() ;(2)成立;证明见解析;(3)
;(2)成立;证明见解析;(3)![]() .
.
【解析】
(1)将△ABE绕点A逆时针旋转90°,得到△ADG,据此知AE=AG,BE=DG,∠BAE=∠DAG,证明△AFE≌△AFG可得EF=FG,从而得出答案.
(2)将△ABE绕点A逆时针旋转![]() 得到△ADH,知∠ABE=∠ADH,∠BAE=∠DAH,AE=AH,BE=DH,证明△AEF≌△AHF得.
得到△ADH,知∠ABE=∠ADH,∠BAE=∠DAH,AE=AH,BE=DH,证明△AEF≌△AHF得.
(3)将△AEC绕点A顺时针旋转90°,得到△![]() ,连接
,连接![]() ,据此知
,据此知![]() ,
,![]() ,∠C=∠
,∠C=∠![]() ,
,![]() ,由
,由![]() 知
知![]() ,即
,即![]() ,从而得到
,从而得到![]() ,易证
,易证![]() 得
得![]() ,根据
,根据![]() 可得答案.
可得答案.
(1)延长![]() 到
到![]() ,使
,使![]() ,连接
,连接![]() ,
,
在正方形![]() 中,
中,
![]() ,
,![]()
在![]() 和
和![]() 中,
中,
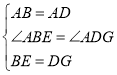
![]()
![]() ,
,
![]() ,
,![]() ,
,
![]()
![]()
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
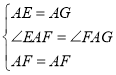
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
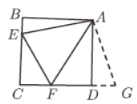
(2)延长![]() 交点
交点![]() ,使
,使![]() ,连接
,连接![]() ,
,
![]()
![]() ,
,
![]() ,
,![]() ,
,
![]()
![]()
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
![]() .
.
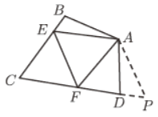
(3)将![]() 绕点
绕点![]() 旋转至
旋转至![]() ,连接
,连接![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]() ,
,![]() ,
,
![]()
![]()
![]() ,
,
![]()
![]() ,
,
![]()
设![]() ,
,
![]() ,
,![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() .
.


科目:初中数学 来源: 题型:
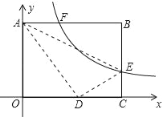
【题目】如图,将矩形ABCO放在平面直角坐标系中,其中顶点B的坐标为(5,3),E是BC边上一点,将△ABE沿AE翻折,点B刚好与OC边上的点D重合,过点E的反比例函数y=![]() 的图象与边AB交于点F,则线段AF的长为_____.
的图象与边AB交于点F,则线段AF的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角三角形ABC中,直线l为BC的中垂线,射线m为∠ABC的角平分线,直线l与m相交于点P.若∠BAC=60°,∠ACP=24°,则∠ABP的度数是( )

A. 24° B. 30° C. 32° D. 36°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=14.5米,NF=0.2米.设太阳光线与水平地面的夹角为α,当α=56.3°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的NF这层上晒太阳.

(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问小猫能否还晒到太阳?请说明理由.(参考数据:sin56.3°≈0.83,cos56.3°≈0.55,tan56.3°≈1.5)
查看答案和解析>>
科目:初中数学 来源: 题型:
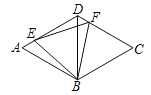
【题目】如图所示,△ABD和△BCD都是等边三角形,E、F分别是边AD、CD上的点,且DE=CF,连接BE、EF、FB.
求证:(1)△ABE≌△DBF;
(2)△BEF是等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
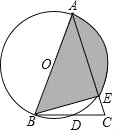
【题目】如图,在△ABC中,AB=AC,E在AC上,经过A,B,E三点的圆O交BC于点D,且D点是弧BE的中点,
(1)求证AB是圆的直径;
(2)若AB=8,∠C=60°,求阴影部分的面积;
(3)当∠A为锐角时,试说明∠A与∠CBE的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在坡顶![]() 处的同一水平面上有一座古塔
处的同一水平面上有一座古塔![]() ,数学兴趣小组的同学在斜坡底
,数学兴趣小组的同学在斜坡底![]() 处测得该塔的塔顶
处测得该塔的塔顶![]() 的仰角为
的仰角为![]() ,然后他们沿着坡度为
,然后他们沿着坡度为![]() 的斜坡
的斜坡![]() 攀行了
攀行了![]() 米,在坡顶
米,在坡顶![]() 处又测得该塔的塔顶
处又测得该塔的塔顶![]() 的仰角为
的仰角为![]() .求古塔
.求古塔![]() 的高度.(结果精确到
的高度.(结果精确到![]() 米,参考数据:
米,参考数据: ![]() ,
, ![]() ,
, ![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
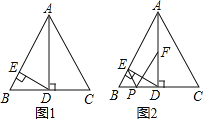
【题目】如图1,△ABC是边长为8的等边三角形,AD⊥BC下点D,DE⊥AB于点E
(1)求证:AE=3EB;
(2)若点F是AD的中点,点P是BC边上的动点,连接PE,PF,如图2所示,求PE+PF的最小值及此时BP的长;
(3)在(2)的条件下,连接EF,若AD=![]() ,当PE+PF取最小值时,△PEF的面积是 .
,当PE+PF取最小值时,△PEF的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设二次函数 y=ax2+bx﹣(a+b)(a,b 是常数,a≠0).
(1)判断该二次函数图象与 x 轴的交点的个数,说明理由.
(2)若该二次函数图象经过 A(﹣1,4),B(0,﹣1),C(1,1)三个点中的其中两个点,求该二次函数的表达式.
(3)若 a+b<0,点 P(2,m)(m>0)在该二次函数图象上,求证:a>0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com