
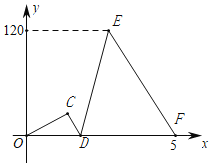
【题目】甲乙两人同时开车从A地出发,沿一条笔直的公路匀速前往相距400千米的B地,1小时后,甲发现有物品落在A地,于是立即按原速返回A地取物品,取到物品后立即提速25%继续开往B地(所有掉头和取物品的时间忽略不计),甲乙两人间的距离y千米与甲开车行驶的时间x小时之间的部分函数图象如图所示,当甲到达B地时,乙离B地的距离是_____.

【答案】40
【解析】
结合题意分析函数图象:线段OC对应甲乙同时从A地出发到A返回前的过程,此过程为1小时;线段CD对应甲返回走到与乙相遇的过程(即甲的速度大于乙的速度);线段DE对应甲与乙相遇后继续返回走至到达A地的过程,因为速度相同,所以甲去和回所用时间相同,即x=2时,甲回到A地,此时甲乙相距120km,即乙2小时行驶120千米;线段EF对应甲从A地重新出发到追上乙的过程,即甲用(5﹣2)小时的时间追上乙,可列方程求出甲此时的速度,进而求出甲到达B地的时刻,再求出此时乙所行驶的路程.
解:∵甲出发到返回用时1小时,返回后速度不变,
∴返回到A地的时刻为x=2,此时y=120,
∴乙的速度为60千米/时,
设甲重新出发后的速度为v千米/时,列得方程:
(5﹣2)(v﹣60)=120,
解得:v=100,
设甲在第t小时到达B地,列得方程:
100(t﹣2)=400
解得:t=6,
∴此时乙行驶的路程为:60×6=360(千米),
乙离B地距离为:400﹣360=40(千米).
故答案为:40.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】根据以下10个乘积,回答问题:
11×29;12×28;13×27;14×26;15×25;16×24;17×23;18×22;19×21;20×20.
(1)将以上各乘积分别写成“a2﹣b2”(两数平方)的形式,将以上10个乘积按照从小到大的顺序排列起来;
(2)用含有a,b的式子表示(1)中的一个一般性的结论(不要求证明);
(3)根据(2)中的一般性的结论回答下面问题:某种产品的原料提价,因而厂家决定对产品进行提价,现有两种方案方案:第一次提价p%,第二次提价q%;方案2:第一、二次提价均为![]() %,其中p≠q,比较哪种方案提价最多?
%,其中p≠q,比较哪种方案提价最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,AB=AC=10,线段BC在轴上,BC=12,点B的坐标为(﹣3,0),线段AB交y轴于点E,过A作AD⊥BC于D,动点P从原点出发,以每秒3个单位的速度沿x轴向右运动,设运动的时间为t秒.

(1)点E的坐标为( , );
(2)当△BPE是等腰三角形时,求t的值;
(3)若点P运动的同时,△ABC以B为位似中心向右放大,且点C向右运动的速度为每秒2个单位,△ABC放大的同时高AD也随之放大,当以EP为直径的圆与动线段AD所在直线相切,求t的值和此时C点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形,建立如图所示的平面直角坐标系,点C的坐标为(0,﹣1).
(1)在如图的方格纸中把△ABC以点O为位似中心扩大,使放大前后的位似比为1:2,画出△A1B1C1(△ABC与△A1B1C1在位似中心O点的两侧,A,B,C的对应点分别是A1,B1,C1).
(2)利用方格纸标出△A1B1C1外接圆的圆心P,P点坐标是 ,⊙P的半径= .(保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,若∠DAB的平分线AE交CD于E,连结BE,且BE也平分∠ABC,则以下的命题中正确的个数是( )
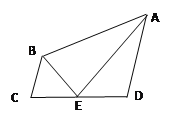
①BC+AD=AB ; ②E为CD中点
③∠AEB=90°; ④S△ABE=![]() S四边形ABCD
S四边形ABCD
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
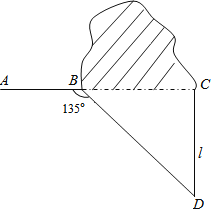
【题目】如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线L,过点B作一直线(在山的旁边经过),与L相交于D点,经测量∠ABD=135°,BD=800米,求直线L上距离D点多远的C处开挖?(![]() ≈1.414,精确到1米)
≈1.414,精确到1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宜兴在“创建文明城市”行动中,某社区计划对面积为2160m2的区域进行绿化.经投标,由甲、乙两个工程队来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为480m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积;
(2)设甲工程队施工x天,乙工程队施工y天,刚好完成绿化任务,求y与x的函数表达式;
(3)若甲队每天绿化费用是0.8万元,乙队每天绿化费用为0.35万元,且甲、乙两队施工的总天数不超过26天,则如何安排甲乙两队施工的天数,使施工总费用最低?并求出最低费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com